Solveeit Logo
Login

Question

Question: How do you find the slope given \(\left( -2,-2 \right)\) and\(\left( -2,4 \right)\)? \[\]...

How do you find the slope given (−2,−2)\left( -2,-2 \right) and(−2,4)\left( -2,4 \right)? $$$$

Explanation

Solution

We recall the definition of slope form slope of point equation. We use the formula for slope of line joining two points (x1,y1),(x2,y2)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right) that is m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} to find the slope of line joining the given points (−2,−2)\left( -2,-2 \right) and(−2,4)\left( -2,4 \right) .$$$$

Complete step-by-step solution:
We know from the Cartesian coordinate system that every linear equation can be represented as a line. If the line is inclined with positive x−x-axis at an angle θ\theta then its slope is given by m=tan⁡θm=\tan \theta and if it cuts y−y-axis at a distance cc from the origin the intercept is given by cc. The slope-intercept form of equation is given by
y=mx+cy=mx+c
The slope mm here means rise over run which means to what extent the line raised itself above the positive x−x-axis with respect to the extension in the x−x-axis. If m=0m=0 we get a line parallel to x−x-axis .We know that if the slope which undefined which means m=∞m=\infty we get a line perpendicular to x−x-axis and if m=0m=0 we get a line parallel to x−x-axis.$$$$
We know that when we are given a line joining two points (x1,y1),(x2,y2)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right) in plane then we can find the slope of the line as the ratio of horizontal range y2−y1{{y}_{2}}-{{y}_{1}} and vertical range x2−x1{{x}_{2}}-{{x}_{1}} which means
m=y2−y1x2−x1m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}
We are given the coordinates of two points (−2,−2)\left( -2,-2 \right) and(−2,4)\left( -2,4 \right). So we have x1=−2,y1=−2,x2=−2,y2=4{{x}_{1}}=-2,{{y}_{1}}=-2,{{x}_{2}}=-2,{{y}_{2}}=4. So the slope of the line is
m=y2−y1x2−x1=4−(−2)−2−(−2)=60=∞m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{4-\left( -2 \right)}{-2-\left( -2 \right)}=\dfrac{6}{0}=\infty
So the slope is undefined and hence the line perpendicular to x−x-axis.

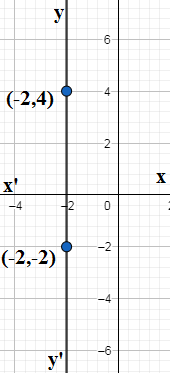
Note: We note that line passing given two points has the equation x=−2x=-2.The slope determines the orientation and inclination of the line. We note that if the slope is m>0m > 0 positive then we get a line increasing from left to right. If the slope is negative that is m<0m < 0 we get a line decreasing from left to right.