Question

How do you find the slope and y-intercept to sketch $y=3x-1$?

Answer 1

The slope of a graph is defined as the derivative of y with respect to x. So we need to differentiate both the sides of the given equation of the line from which we will obtain the value of the slope. And the y-intercept is the point where the graph cuts the y-axis. Therefore, on putting $x=0$ in the given equation we will obtain the value of the y-intercept. From these values of the slope and the y-intercept, we will be able to sketch the graph.

Complete step by step solution:
The equation given in the above question is
$\Rightarrow y=3x-1.......\left( i \right)$
We know that the slope of a graph is equal to the derivative of y with respect to x. Therefore, we differentiate the above equation with respect to x to get
$\begin{aligned} & \Rightarrow \dfrac{dy}{dx}=3 \\\ & \Rightarrow m=3 \\\ \end{aligned}$
Thus, the slope is equal to $3$.
Now, we know that the y-intercept is the point where the graph cuts the y-axis. Since the equation of y-axis is $x=0$, we substitute it in the equation (i) to get
$\begin{aligned} & \Rightarrow y=3\left( 0 \right)-1 \\\ & \Rightarrow y=-1 \\\ \end{aligned}$
So the y-intercept is equal to $-1$.
From these values of the slope and the y-intercept, we can sketch the graph as shown below.

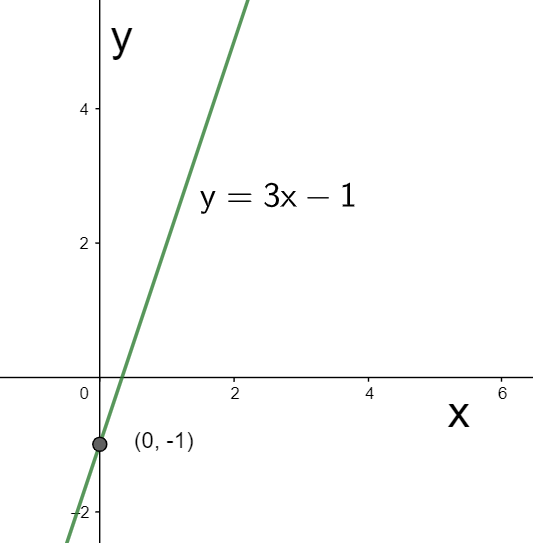
Hence, we have sketched the graph of $y=3x-1$.

Note: The values of the slope and the y-intercept can be easily evaluated by comparing the given equation of line with the slope-intercept equation of a line, which is given by $y=mx+c$. Here m is the slope, and c is the y-intercept.