Question

How do you find the slope and y-intercept of $5x-2=0$?

Answer 1

We first try to find the characteristics of the line $5x-2=0$. We find the relation of the slope of the line with the angle it makes with the positive X-axis. We also find the point at which it intersects the Y-axis.

Complete step-by-step solution:
We need to find the slope and y-intercept of the function $5x-2=0$.
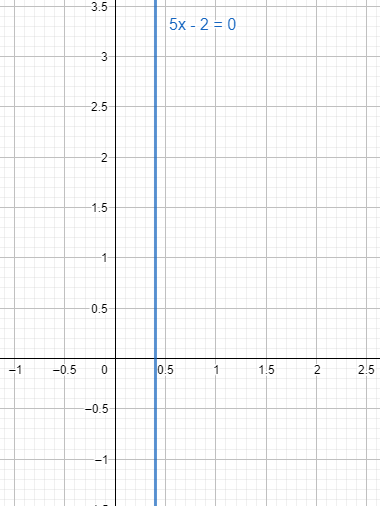
The given line $5x-2=0$ can be converted to $x=\dfrac{2}{5}$.
We know that any equation of the form $x=c$ where $c$ is a constant will be a vertical line parallel to the Y-axis. The slope of these equations is always undefined.
Slope is usually defined by the ratio tan of the angle made by a line with the positive X-axis.
In case of vertical lines, they make ${{90}^{\circ }}$ with the X-axis.
We also know $\tan 90$ is undefined. Therefore, the slope of $5x-2=0$ is undefined.
Now we find the y-intercept of $5x-2=0$.
As we know that the line is parallel to the Y-axis and we know that parallel lines don’t touch or intersect each other ever. Therefore, there is no y-intercept of the function $5x-2=0$.

Note: We can also take the equation as a function of $x$ where $f\left( x \right)=5x-2$. We know that the slope of any function is the differentiated form of the function equal to $\dfrac{dy}{dx}$. In the function of as function $y$ is not mentioned and we have that $5x-2=0$, we can convert the equation to $x=\dfrac{2}{5}$ which gives $dx=0$. Division by zero is undefined. Therefore, the slope for $5x-2=0$ is undefined.