Question

How do you find the slope and $y$ intercept of $2x+2y=8$ ?

Answer 1

Problems on coordinate geometry can be easily solved by converting the given equation as the slope and $y$ intercept form. Then, we compare the given equation to the general equation of the same type. As, the given equation is of a straight line we compare $2x+2y=8$ with the general equation of a straight line, i.e., $y=mx+c$

Complete step-by-step solution:
The given equation we have is
$2x+2y=8$
As, the given equation is not in the slope and $y$ intercept form we convert the equation in the slope and $y$ intercept form as
$\Rightarrow 2y=8-2x$
$\Rightarrow y=-\dfrac{2x}{2}+\dfrac{8}{2}$
$\Rightarrow y=-x+4....expression1$
The above equation is now converted into the slope and $y$ intercept form. So, we will compare it with the general equation of a straight line
$y=mx+c....\text{expression}2$
Here, the $m$ represents the slope (angle made by the line with $x$ -axis) of the straight line. Also, if we put $x=0$ in the equation we see that $y=c$ . Hence, $c$ is the $y$ intercept of the line.
Now, comparing $\text{expression}1$ and $\text{expression2}$, we get
$m=-1$ and $c=4$
Therefore, we can conclude to the result that the given straight line has a $\text{slope, }m=-1$ and $y$ intercept, $c=4$.

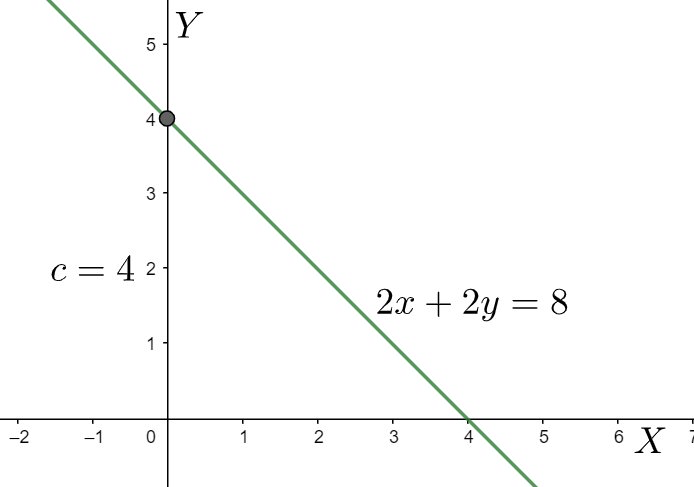
Note: Before comparing the straight-line equation with the general form, we must check whether the equation is in the slope and $y$ intercept form. Otherwise, we need to convert the given equation into the slope and $y$ intercept form and then compare it with $y=mx+c$. Also, this problem can be solved with the help of another method i.e., Graphical method. First, we have to find out any two points which satisfies the equation and then plot it on graph paper. Connecting the two points we get the line on the graph paper. Now, we will be able to find the slope of the line by measuring the angle with a protector and the $y$ intercept by measuring the length of the $y\text{-axis}$ up to the point it is cut by the line.