Question

How do you find the slope and the y-intercept for the line $5x - y + 2 = 0$?

Answer 1

Here in this question, we have to plot the graph for the equation using the slope and the intercept. By substituting the x is equal to zero we can find the y intercept value and substituting y is equal to zero we can find the x intercept value. By equating the given equation to the general equation of line we can determine the slope.

Complete step-by-step solution:
The given equation must be written in the form of $y = mx + b$, where m is slope and b is known as y-intercept. Slope means ratio of vertical change to the horizontal change i.e., ratio of change in y-axis or step size of y-axis to the change in x-axis or step size of x-axis. An intercept is a point where the straight line or a curve intersects the y-axis in a plane. If the point x is zero then the obtained point is a y -intercept.
Now consider the given equation $5x - y + 2 = 0$
This can be written as $y = 5x + 2$-------(1)
Substitute the value of x as 0 in equation (1), then we have
$\Rightarrow y = 5(0) + 2$
On simplifying we get
$\Rightarrow y = 2$
Therefore, y-intercept is (0, 2)
Substitute the value of y as 0 in the equation (1) then we have
$\Rightarrow 0 = 5x + 2$
On simplifying we get

$$\Rightarrow - 2 = 5x \\\ \Rightarrow x = \dfrac{{ - 2}}{5} \\\ \Rightarrow x = - 0.4 \\\$$

Therefore, x-intercept is (-0.4, 0)
The general equation of a line is given by $y = mx + b$, the b is the y-intercept and it is 2. On substituting we get $y = mx + 2$ ------ (2)
On comparing the equation (1) and equation (2) we get
$m = 5$
Therefore, the slope is $5$
The graph for this is given below

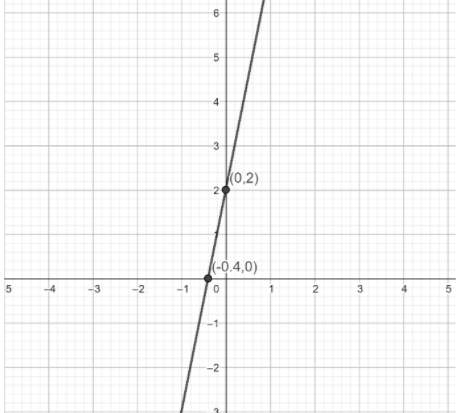
Note: The question is belonging to the concept of graph. By comparing the given equation to the equation of a line we calculate the slope and intercept. Or by choosing the value of x we can determine the value of y and then plotting the graphs for these points we obtain the result.