Question

How do you find the slope and intercepts to the graph f(x)=3-2x?

Answer 1

This type of question is based on the concept of equation of lines. We are given the equation of line is f(x)=3-2x. Let us first substitute f(x) as y. We know that the slope-intercept form of the equation of line is y=mx+c, where m is the slope of the line and c is the y-intercept of the line. On comparing the slope intercept form of the line with the given line, we get m=-2 and c=3. Thus, we get that the slope of the equation is -2 and the y-intercept is 3. Now, we have to find the x-intercept by substituting y=0 in the given equation. Add 2x on both the sides of the equation and divide the whole expression by 2 to find the x-intercept.

Complete step by step solution:
According to the question, we are asked to find the slope and intercept of the line equation f(x)=3-2x.
We have been given the equation of line is f(x)=3-2x. ------------(1)
Let us first substitute f(x) as y.
Therefore, we get y=3-2x. -------------(2)
Let us plot the graph of y=3-2x.

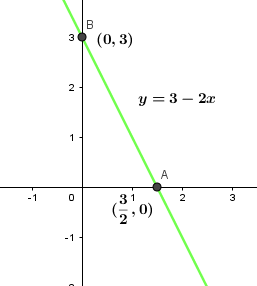
We know that the slope intercept form of the equation is y=mx+c, where m is the slope of the line and c is the y-intercept of the equation, that is the line crosses the y-axis at (0,c).
We find that the coefficient of x in equation (2) is -2 which is the slope of the equation.
Therefore, we get that the slope m=-2.
Now, we have to find the intercepts of the equation.
We know that the constant c in the slope intercept form is the y-intercept.
From equation (2), we get that the constant is 3.
That is, the y-intercept of the line is equal to 3.
Therefore, we get c=3. And the y intercept is at (0,3).
Now, we have to find the x-intercept.
To find the x-intercept, we have to substitute the value of y as 0.
$\Rightarrow 3-2x=0$
Add 2x on both the sides of the equation.
$\Rightarrow 3-2x+2x=0+2x$
On further simplifications, we get
3=2x
We can write the expression as 2x=3.
Divide the expression by 2.
$\Rightarrow \dfrac{2x}{2}=\dfrac{3}{2}$
We find that 2 are common in both the numerator and denominator of the LHS. On cancelling 2, we get
$x=\dfrac{3}{2}$
Therefore, we get that the x-intercept is at $\left( \dfrac{3}{2},0 \right)$
Therefore, the slope of the line f(x)=3-2x is -2 and the x and y intercepts are at $\left( \dfrac{3}{2},0 \right)$ and (0,3) respectively.

Note:
Whenever we get such types of problems, we have to make certain substitutions and convert the given equation to the form y=mx+c. We should find the intercepts of x and y separately since it is mentioned in the question. Avoid calculation mistakes based on sign conventions. We can also check the obtained answer by comparing the intercepts with the graph.