Question

How do you find the slope and intercepts to graph $2x-3y=3$?

Answer 1

In this problem we need to calculate the slope and the intercepts of the given line. We can solve this problem in many methods. We will follow the easiest one for this time. The solution contains two parts, one part is finding the slope and the second part is finding the intercepts. For slope of the given line, we will convert the given equation in slope intercept form which is $y=mx+c$. So, we will convert the given equation in the form of $y=mx+c$ where $m$ is our required slope of the line. Now the first part is over. In the second part we will calculate the intercepts of the line. For this also we will convert the given equation into intercept form which is $\dfrac{x}{a}+\dfrac{y}{b}=1$ where $a$ is the value of $x$ intercept and $b$ is the value of $y$ intercept.

Complete answer:
The equation of the line is $2x-3y=3$.
Calculating the slope of the given line.
To calculate the slope of the line we will convert the given equation in slope intercept form which is $y=mx+c$.
Shifting the term $2x$ which is in right side to left side, then we will get
$\begin{aligned} & 2x-3y=3 \\\ & \Rightarrow -3y=3-2x \\\ \end{aligned}$
Dividing the above equation with $-3$ on both sides of the above equation, then we will get
$\begin{aligned} & \Rightarrow \dfrac{-3y}{-3}=\dfrac{3-2x}{-3} \\\ & \Rightarrow y=\dfrac{3}{-3}+\dfrac{2x}{3} \\\ & \Rightarrow y=\left( \dfrac{2}{3} \right)x-1 \\\ \end{aligned}$
Comparing the above equation with $y=mx+c$, then we will get the slope of the equation as $m=\dfrac{2}{3}$.
Now we will calculate the intercepts of the given equation by converting the equation into intercept form which is $\dfrac{x}{a}+\dfrac{y}{b}=1$.
Dividing the given equation $2x-3y=3$ with $3$ on both sides, then we will get
$\begin{aligned} & \Rightarrow \dfrac{2x-3y}{3}=\dfrac{3}{3} \\\ & \Rightarrow \left( \dfrac{2}{3} \right)x+\left( \dfrac{-3}{3} \right)y=1 \\\ & \Rightarrow \dfrac{x}{\left( \dfrac{3}{2} \right)}+\dfrac{y}{\left( -1 \right)}=1 \\\ \end{aligned}$
From the above equation we can write $x$ intercept of the given equation as $\dfrac{3}{2}$, $y$ intercept of the given equation as $-1$.

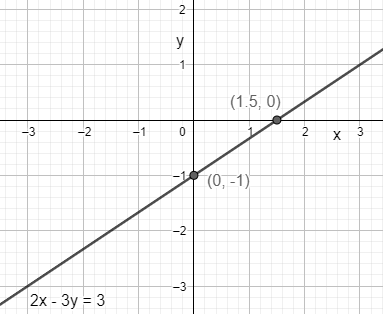
Note: In this problem we have calculated the slope and intercept by converting the given equation into various forms. We know that the slope of the equation is the variation in the direction of $y$ for a unit variation in $x$. So, we will calculate any two points on the given line and calculate the value of $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and consider it as required slope. To calculate the intercepts we will substitute $x=0$ and calculate the $y$ for $y$ intercept and for $x$ intercept we will substitute $y=0$ and calculate the $x$ value.