Question

How do you find the slope and intercept to graph $2x - y = 1$?

Answer 1

Hint : In order to find the slope and intercept to graph the line $2x - y = 1$, we will convert the given line into the slope- intercept form i.e., $y = mx + b$. Then, we will compare both to determine the value of $m$ which is the slope and value of $b$ which is the $y$- intercept. Then, we know the $y$- intercept is the point where the line intersects the $y$-axis. And also, Slope is the ‘steepness’ of the line, also commonly known as rise over run i.e., $\dfrac{{rise}}{{run}}$. By using these we will determine the two points of the line and finally plot these graphically.

Complete step-by-step answer :
Here, we will graph $2x - y = 1$.
Now, we will write the equation in the slope- intercept form i.e., $y = mx + b$ $\to \left( 1 \right)$
Where the $m$ is the slope
$b$ is the $y$- intercept
Then, we have $- y = - 2x + 1$
$- y = - \left( {2x - 1} \right)$
$y = 2x - 1$ $\to \left( 2 \right)$
By comparing equation $\left( 1 \right)$ and $\left( 2 \right)$, we have
$m = 2$ i.e., the slope of the equation
$b = - 1$ i.e., the $y$- intercept
The $y$- intercept is the point where the line intersects the $y$-axis.
Therefore, the point is $\left( {0, - 1} \right)$.
Slope is the ‘steepness’ of the line, also commonly known as rise over run i.e., $\dfrac{{rise}}{{run}}$. Here, $m = 2$ therefore, we can say that the graph “rise” $2$ point upwards and “runs” $1$ points to the right from the $y$- intercept.
Now, we know the slope and the $y$- intercept, thus we also know that $\left( {0 + 1, - 1 + 2} \right) = \left( {1,1} \right)$ which will also be on the line.
Now, we know two points of the equation i.e., $\left( {0, - 1} \right)$ and $\left( {1,1} \right)$.
Let us plot these points graphically,

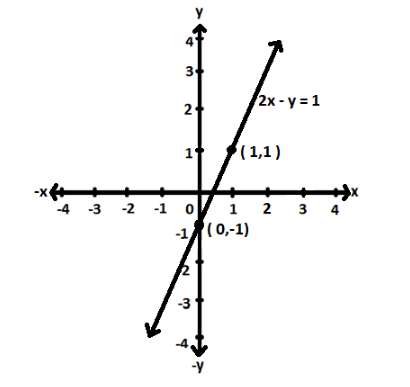
Note : Equation of straight line is usually written in the slope-intercept form. When we are given an equation in slope- intercept form, we can use the $y$- intercept as the point, then out the slope from there. When an equation of a line is not given in slope-intercept form, our first step will be to solve the equation for $y$. Sometimes the slope intercept form will be called as $y$-form.