Question

How do you find the slope and intercept of $y=-\dfrac{3}{5}x+2$?

Answer 1

In this problem we need to calculate the slope and intercept of the given linear equation. For this we are going to find any two points on the given line. So, we will assume various values of the $x$ and substitute them in the given equation of the line and calculate the value of $y$. From those values we can write the points on the line as $\left( x,y \right)$. Here we need to calculate the slope of the equation which can be written as $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ are the two points on the line. to calculate the intercept of the given equation we will calculate the value of $y$ at $x=0$.

Complete step by step solution:
The equation of the line is $y=-\dfrac{3}{5}x+2$.
Let us calculate the value of $y$ at $x=0$ by substituting the value of $x$ in the given line equation, then we will get
$\begin{aligned} & \Rightarrow y=-\dfrac{3}{5}\left( 0 \right)+2 \\\ & \Rightarrow y=2 \\\ \end{aligned}$
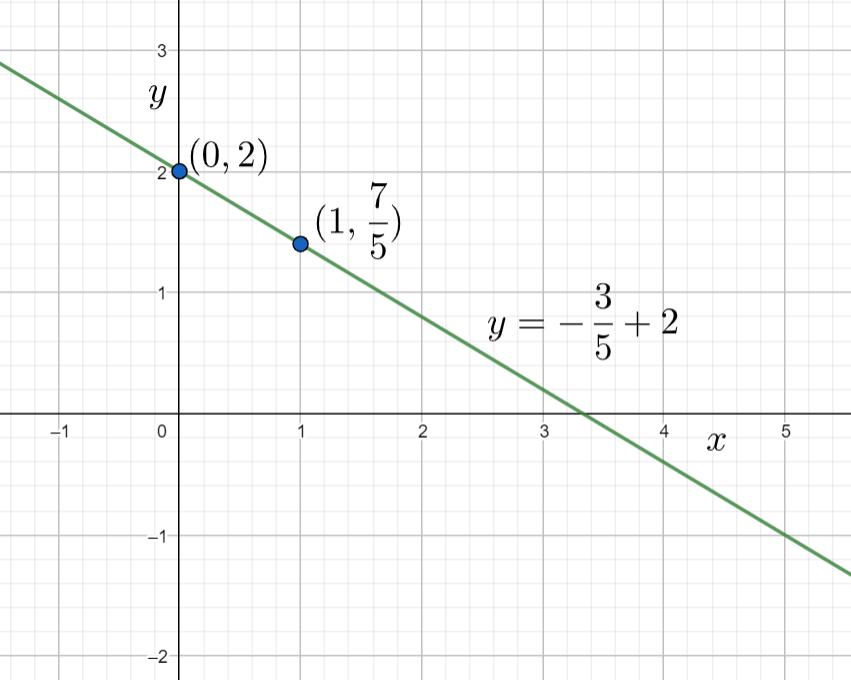
Hence the point on the line is $\left( 0,2 \right)$.
Let us again calculate the value of $y$ at $x=1$ by substituting the value of $x$ in the given line equation, then we will get
$\begin{aligned} & \Rightarrow y=-\dfrac{3}{5}\left( 1 \right)+2 \\\ & \Rightarrow y=-\dfrac{3}{5}+2 \\\ & \Rightarrow y=\dfrac{-3+10}{5} \\\ & \Rightarrow y=\dfrac{7}{5} \\\ \end{aligned}$
Hence the point on the line is $\left( 1,\dfrac{7}{5} \right)$.
Now the slope of the given line which passes through $\left( 0,2 \right)$, $\left( 1,\dfrac{7}{5} \right)$ will be
$\begin{aligned} & \Rightarrow m=\dfrac{\dfrac{7}{5}-2}{1-0} \\\ & \Rightarrow m=\dfrac{7-10}{5} \\\ & \Rightarrow m=-\dfrac{3}{5} \\\ \end{aligned}$
Now the value of $y$ at $x=0$ is $2$.
Hence the slope of the given line is $-\dfrac{3}{5}$, intercept is $2$ and the graph of the given line will be

Note: From the given equation also, we can calculate the required data. If we observe the equation it is in slope intercept form so we can compare the given equation with $y=mx+c$ and write the values of slope $\left( m \right)$ and intercept $\left( c \right)$.