Question

How do you find the slope and intercept of $3x-y=5$?

Answer 1

First we will convert the given equation into a general slope-intercept form of a line. The general equation of slope-intercept form of a line is given as $y=mx+c$ where, m is the slope of line and c is the y-intercept of the line. Then by comparing the values we get the desired answer.

Complete step by step solution:
We have been given an equation $3x-y=5$.
We have to find the slope and intercept of the given equation.
We know that the slope-intercept form of a line is given by the equation $y=mx+c$ where, m is the slope of line and c is the y-intercept of the line. Y-intercept of the line is the point where a line crosses the Y-axis.
Now, let us convert the given equation in the general form. Then we will get
$\begin{aligned} & \Rightarrow 3x-y=5 \\\ & \Rightarrow 3x-5=y \\\ & \Rightarrow y=3x-5 \\\ \end{aligned}$
Now, comparing the given equation with the general equation we will get
$\Rightarrow m=3$ and $\Rightarrow c=-5$
Hence we get the values of slope as 3 and value of y-intercept of the given line as $-5$.
The slope and y-intercept of the line $3x-y=5$ are 3 and $-5$ respectively.

Note: Alternatively we can find the slope and intercept of the given equation by using the graphing method. For this we draw the graph of the given equation which is a straight line and then we can find the slope and intercept of the obtained line.

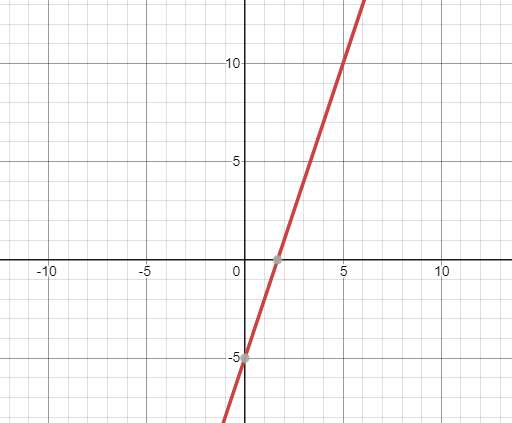
Here the graph intersecting the y-axis at (-5,0), Hence -5 is the intercept.