Question

How do you find the slope and intercept of $3x - y = 5$?

Answer 1

In this question, we have to make a given equation in the form of slope intercept form of a line. It can be done by first subtracting $3x$ from both sides of the given equation. Then, multiplying each term in $- y = 5 - 3x$ by $- 1$. Then compare the final equation with the standard slope intercept form of a line and find the slope $m$ and an intercept $c$ on $y$-axis for this equation.

Formula used:
The Slope Intercept Form of a Line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.

Complete step by step solution:
We know that the slope intercept form of a line is the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Given equation is $3x - y = 5$
So, we have to make a given equation in the form of $y = mx + c$, the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis.
Subtract $3x$ from both sides of the given equation.
$\Rightarrow - y = 5 - 3x$
Multiply each term in $- y = 5 - 3x$ by $- 1$.
$\Rightarrow \left( { - y} \right) \times \left( { - 1} \right) = 5 \times \left( { - 1} \right) - 3x \times \left( { - 1} \right)$
Multiply $- y$ by $- 1$.
$\Rightarrow y = 5\left( { - 1} \right) - 3x\left( { - 1} \right)$
Multiply $5$ by $- 1$.
$\Rightarrow y = - 5 - 3x\left( { - 1} \right)$
Multiply $- 3x$ by $- 1$.
$\Rightarrow y = - 5 + 3x$
Reorder $- 5$ and $3x$.
$\Rightarrow y = 3x - 5$
Now, compare this equation with the standard slope intercept form of a line and find the slope $m$ and an intercept $c$ on $y$-axis for this equation.
Here, $m = 3$ and $c = - 5$.

Therefore, the slope of the given line is $3$ and $y$-intercept is $- 5$.

Note: Slope and $y$-intercept of a line can also be determined by graphing the given equation.
Graph of $3x - y = 5$:

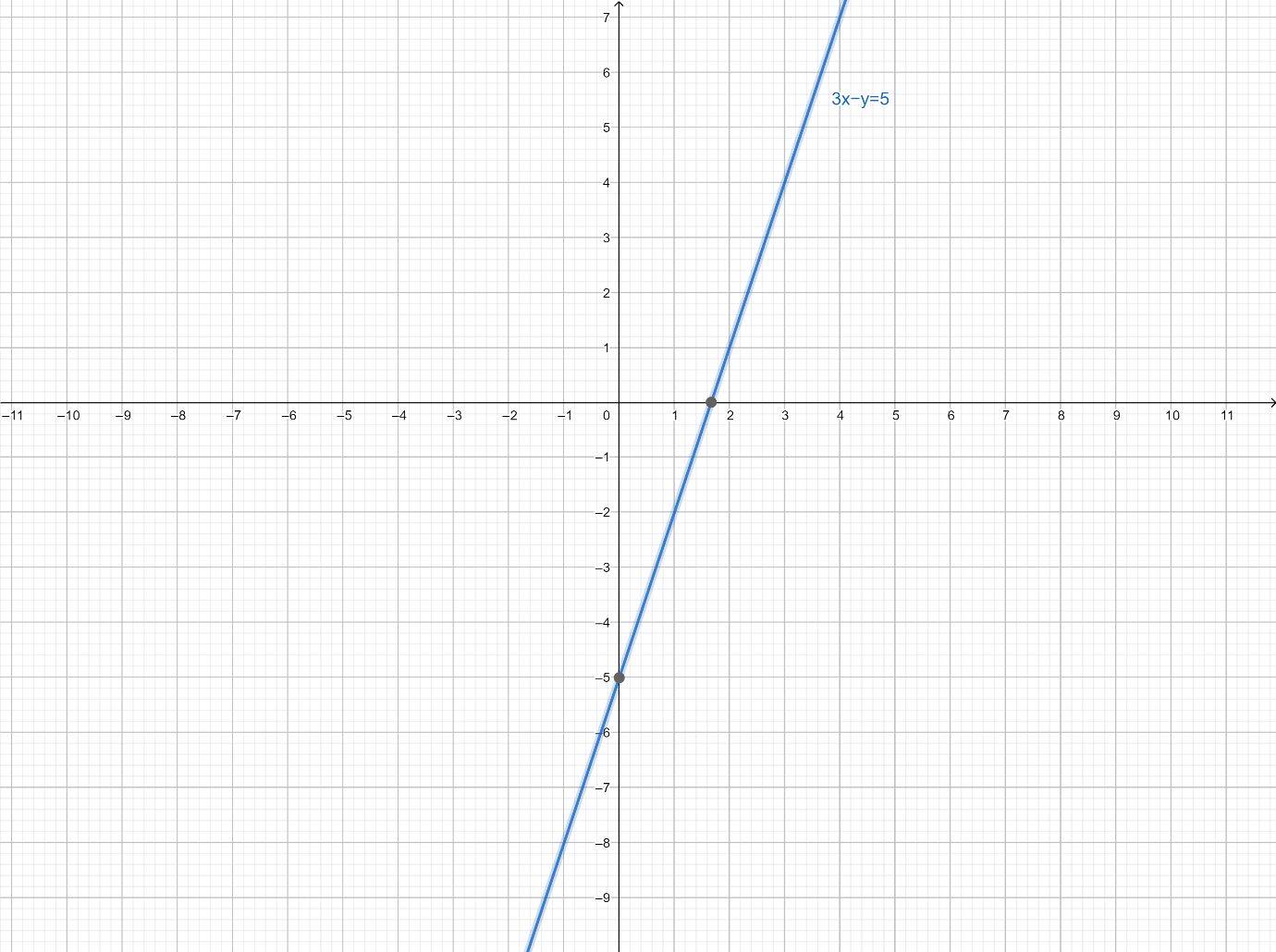
Since, the line $3x - y = 5$ cuts the $y$-axis at $- 5$.
So, $y$-intercept of a given line is $- 5$.
We can find the slope of given line by putting $\left( {{x_1},{y_1}} \right) = \left( {2,0} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {0, - 5} \right)$ in $\Rightarrow m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$.
So, slope is
$\Rightarrow m = \dfrac{{ - 5 - 0}}{{0 - \dfrac{5}{3}}}$
On simplification, we get
$\Rightarrow m = 5 \times \dfrac{3}{5}$
$\Rightarrow 3$
So, the slope of the given line is $3$.
Therefore, the slope of the given line is $3$ and $y$-intercept is $- 5$.