Question

How do you find the slope and intercept for $8x-2y=14$?

Answer 1

This question is from the topic of straight line. In solving this question, we will first know about the general form of straight line. From there, we will find out the slope of the equation which is given in the question. After that, in the given equation we will put the value of x as zero and find the value of y. After that, in the given equation we will put the value of y as zero and find the value of x. After that, we will get the intercepts.

Complete step by step answer:
Let us solve this question.
In this question, we have asked to find the slope and the intercept for the equation $8x-2y=14$.
The general equation of straight line is
$ax+by=c$
Where slope of the above equation is $m=-\dfrac{a}{b}$
So, the slope of the equation $8x-2y=14$ will be
$m=-\dfrac{a}{b}=-\left( \dfrac{8}{-2} \right)$
The above can also be written as
$\Rightarrow m=-\left( -\dfrac{8}{2} \right)=\dfrac{8}{2}=4$
Now, for the intercepts we will put the value of x and y as zero and find the value of y and x respectively.
So, let us put x=0 in the equation $8x-2y=14$, we will get
$8\times 0-2y=14$
The above can also be written as
$\Rightarrow -2y=14$
From the above, we get the value of y=-7.
Now, let us put y=0 in the equation $8x-2y=14$, we will get
$8x-2\times 0=14$
The above can also be written as
$\Rightarrow 8x=14$
The above can also be written as
$\Rightarrow x=\dfrac{14}{8}=\dfrac{7}{4}$
Hence, we get that the slope of the equation $8x-2y=14$ is 4. The x-intercept is $\dfrac{7}{4}$ and y-intercept is $-7$.
We can take reference from the following figure:

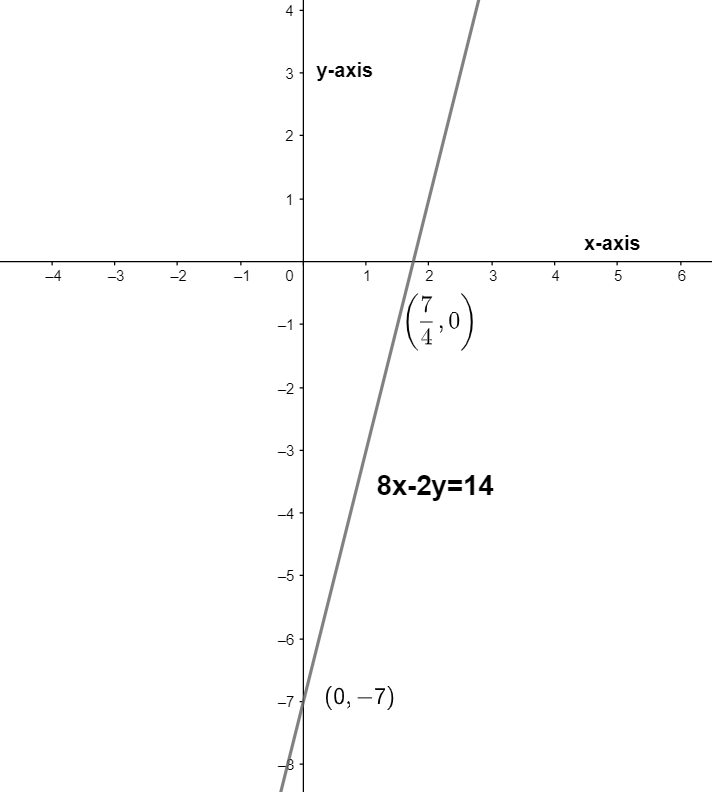
Note: We should have a better knowledge in the topic of straight line to solve this type of question easily. We should know that the general equation of straight line is:
$ax+by=c$
Where, the slope of the above equation is: $m=-\dfrac{a}{b}$
The y-intercept is: $\dfrac{c}{b}$
The x-intercept is: $\dfrac{c}{a}$