Question

How do you find the remaining trigonometric functions of θ given $\cos \theta =\dfrac{-20}{29}$ and θ terminates in Quadrant II ?

Answer 1

As we know in mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, the tan and their reciprocals are the cosec, the sec, the cot respectively.

Complete step-by-step solution:
According to the question we have found the remaining trigonometric functions in the second quadrant. Basically there are four quadrants in which the first quadrant all trigonometric functions are positive, in the second quadrant only sine and cosec are positive, rest all are negative, in third quadrant tan and cot are positive and in fourth quadrant cos and sec are positive.
We have been given that $\cos \theta =\dfrac{-20}{29}$, now to solve the remaining trigonometric functions we will use some formulas of trigonometry.
Given that
$\Rightarrow \cos \theta =\dfrac{-20}{29}$
We know that ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$ or we can write it as:
$\begin{aligned} & \Rightarrow {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \\\ & \Rightarrow \sin \theta =\sqrt{1-{{\cos }^{2}}\theta } \\\ \end{aligned}$
Now putting the value of $\cos \theta =\dfrac{-20}{29}$ in above expression we get
$\begin{aligned} & \Rightarrow \sin \theta =\sqrt{1-{{\left( \dfrac{-20}{29} \right)}^{2}}} \\\ & \Rightarrow \sin \theta =\sqrt{1-\dfrac{400}{841}} \\\ & \Rightarrow \sin \theta =\sqrt{\dfrac{841-400}{841}}=\sqrt{\dfrac{441}{841}}=\dfrac{21}{29} \\\ & \\\ \end{aligned}$
Since in second quadrant sin and its reciprocal is positive
Now we know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ , put the value of $\sin \theta =\dfrac{21}{29}$ and $\cos \theta =\dfrac{-20}{29}$ we get
$\begin{aligned} & \Rightarrow \tan \theta =\dfrac{21}{29}\times \dfrac{29}{-20} \\\ & \Rightarrow \tan \theta =\dfrac{-21}{20} \\\ \end{aligned}$
Now the reciprocals of the sin, the cos and the tan are:
$\begin{aligned} & \Rightarrow \cos ec\theta =\dfrac{1}{\sin \theta } \\\ & \\\ \end{aligned}$
Put the value of $\sin \theta =\dfrac{21}{29}$ in the above expression, we get
$\Rightarrow \cos ec\theta =\dfrac{29}{21}$
Similarly,
$\Rightarrow \sec \theta =\dfrac{1}{\cos \theta }$
Put the value of $\cos \theta =\dfrac{-20}{29}$in the above expression, we get
$\Rightarrow \sec =\dfrac{-29}{20}$
Again,
$\Rightarrow \cot \theta =\dfrac{1}{\tan \theta }$
Putting the value of $\tan \theta =\dfrac{-21}{20}$ in the above expression we get,
$\Rightarrow \cot =\dfrac{-20}{21}$
Hence we get the all trigonometric functions $\sin \theta =\dfrac{21}{29}$ ,$\tan \theta =\dfrac{-21}{20}$ , $\cos ec\theta =\dfrac{29}{21}$ ,$\sec \theta =\dfrac{-29}{20}$ , $\cot \theta =\dfrac{-20}{21}$.

Note: We can also find the value of trigonometric functions by using Pythagoras theorem. Let me show you how we can find them.
Let draw a right angled triangle ABC

We have given that $\cos \theta =\dfrac{-20}{29}$and we all know the formula to find the value of $\cos \theta =\dfrac{b}{h}$ where $h$ is hypotenuse and $b$ is the base of the above triangle. Now label these values on the right angled triangle.

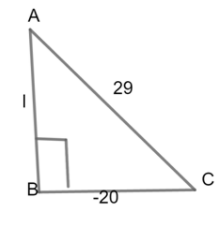
Now we have to find the value of the length by using Pythagora's theorem. The formula of Pythagoras theorem is:
$\Rightarrow {{h}^{2}}={{l}^{2}}+{{b}^{2}}$
To find the value of length we can rewrite it as:
$\begin{aligned} & \Rightarrow {{h}^{2}}-{{b}^{2}}={{l}^{2}} \\\ & \Rightarrow l=\sqrt{{{h}^{2}}-{{b}^{2}}} \\\ \end{aligned}$
Now putting the values of $h$ and$b$, we get
$\begin{aligned} & \Rightarrow l=\sqrt{{{\left( 29 \right)}^{2}}-{{\left( -20 \right)}^{2}}} \\\ & \Rightarrow l=\sqrt{841-400} \\\ & \Rightarrow l=\sqrt{441}=21 \\\ \end{aligned}$
It means the value of length is$21$ . Now we will find the all trigonometric function by using the right angled triangle.
We know
$\Rightarrow \sin \theta =\dfrac{l}{h}$
Now by putting values we get,
$\Rightarrow \sin \theta =\dfrac{21}{29}$
Similarly we can find $\tan \theta =\dfrac{l}{b}$ by putting values, we get
$\begin{aligned} & \Rightarrow \tan \theta =\dfrac{21}{-20} \\\ & \Rightarrow \tan \theta =\dfrac{-21}{20} \\\ \end{aligned}$
And we know
$\begin{aligned} & \Rightarrow \cos ec\theta =\dfrac{1}{\sin \theta } \\\ & \\\ \end{aligned}$
$\Rightarrow \cos ec\theta =\dfrac{29}{21}$
$\Rightarrow \sec \theta =\dfrac{1}{\cos \theta }$
$\Rightarrow \sec =\dfrac{-29}{20}$
$\Rightarrow \cot \theta =\dfrac{1}{\tan \theta }$
$\Rightarrow \cot =\dfrac{-20}{21}$
Hence we get the same trigonometric function as we solved above, $\sin \theta =\dfrac{21}{29}$ ,$\tan \theta =\dfrac{-21}{20}$ , $\cos ec\theta =\dfrac{29}{21}$ ,$\sec \theta =\dfrac{-29}{20}$ , $\cot \theta =\dfrac{-20}{21}$.