Question

How do you find the remaining trigonometric function $\theta$ of given $\cos \theta = \dfrac{{24}}{{25}}$ and $\theta$ terminates in QIV $?$

Answer 1

Hint : In the given question we have to find the remaining different trigonometric function like sin, cos, tan, cot, sec, csc for $\cos \theta = \dfrac{{24}}{{25}}$ and $\theta$ terminates in QIV.
Here $\theta$ terminates in QIV means that $\theta$ terminates in quadrant IV where the abscissa x axis is $+$ and ordinate y axis is $-$ .
Now you should know that $\cos \theta = \dfrac{x}{r}$ , and $\sin \theta = \dfrac{y}{r}$ , where $x,y,r$ are two side and hypotenuse of a right angle triangle. From this you can find value of $\tan \theta ,\cot \theta ,\sec \theta ,\csc \theta$ in terms of $x,y,r$ using identity i.e.
${x^2} + {y^2} = {r^2}$
Because $x,y,r$ are sides of right angled triangle, now solving for $y$ , we get
$y = \pm \sqrt {{r^2} - {x^2}}$
Now you can find the value of all trigonometric functions.

Complete step-by-step answer :
In the given question we have been asked to find the remaining trigonometric functions using $\cos \theta = \dfrac{{24}}{{25}}$ and also $\theta$ terminates in QIV.
Let the point $P(x,y)$ be on a circle of radius r centered at the origin and $P$ is on the terminal ray of $\theta$ . Now let suppose the angle $\theta$ be the non reflex angle from the positive x axis that is coterminal with the angle $\theta$ .
The line segments from $(0,0)$ to $(x,0)$ and to $(0,y)$ form a right angled triangle with hypotenuse $r$ and angle $\theta$ between $x$ and $r$ .
So $\cos \theta = \dfrac{x}{r}$ and $\sin \theta = \dfrac{y}{r}$ .
$x,y,r$ are the lengths of the two sides and the hypotenuse of a right angled triangle respectively.

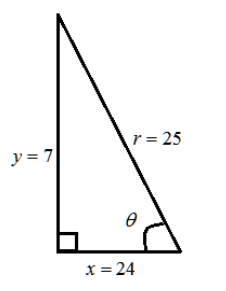
Therefore,
${x^2} + {y^2} = {r^2}$
Now solving for $y$ , we get
$y = \pm \sqrt {{r^2} - {x^2}}$
Now We know the values of $x$ and $r$ , so we can find that value of $y$ using formula i.e.

$$y = \pm \sqrt {{r^2} - {x^2}} \\\ \Rightarrow y = \pm \sqrt {{{25}^2} - {{24}^2}} \\\ \Rightarrow y = \pm 7 \;$$

Now we know that $y$ is negative so $y = - 7$ .
So the value of trigonometric functions will be:

$$\sin \theta = \dfrac{y}{r} = \dfrac{{ - 7}}{{25}} \\\ \tan \theta = \dfrac{y}{x} = \dfrac{{ - 7}}{{24}} \\\ \cot \theta = \dfrac{x}{y} = \dfrac{{24}}{{ - 7}} = \dfrac{{ - 24}}{7} \\\ \sec \theta = \dfrac{1}{x} = \dfrac{25}{{24}} \\\ \csc \theta = \dfrac{1}{y} = \dfrac{25}{{ - 7}} = \dfrac{{ - 25}}{7} \;$$

Hence this is the required answer.

Note : Here you should know that what a right angled triangle is, you should also study the proof of the formula ${x^2} + {y^2} = {r^2}$ which was used in this entire questions. Also the basic trigonometric formula like $\sin \theta = \dfrac{1}{{\csc \theta }},\cos \theta = \dfrac{1}{{\sec \theta }},\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }},\cot \theta = \dfrac{1}{{\tan \theta }}$ .Using these formula you can easily find the solution of these kind of questions.