Question

How do you find the real solutions of the equation by graphing $6{x^2} = 48x$ ?

Answer 1

Hint : In this question, we are given a quadratic equation and we have to find its real solutions by graphing. The solutions of a polynomial equation are defined as those values of x at which the value of y defined in terms of x comes out to be zero. The value of y is zero for the points lying on the x-axis, so the solutions of the given equation will be the x-intercepts of this function. The graph of the equation of the form $a{x^2} + bx + c = 0$ is a parabola.

Complete step by step solution:
We have to find the real solutions of the equation $6{x^2} = 48x$ by graphing.
We will first simplify the equation as –
$6{x^2} = 48x \\\ \Rightarrow {x^2} = 8x \\\ \Rightarrow {x^2} - 8x = 0 \;$
Let ${x^2} - 8x = y$
The graph of this function will be –

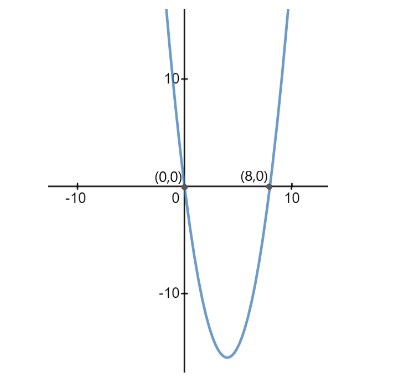
From the graph, we see that the value of y is zero at $x = 0$ and $x = 8$ . They both are real values.
Hence, the real solutions of the equation $6{x^2} = 48x$ are $x = 0$ and $x = 8$ .
So, the correct answer is “ $x = 0$ and $x = 8$ ”.

Note : We can verify if the answer obtained is correct or not by finding out the solutions of the given equation mathematically.
We have ${x^2} - 8x = 0$
Taking “x” common, we get –
$x(x - 8) = 0 \\\ \Rightarrow x = 0,\,x = 8 \;$
Hence, the answer obtained is correct.
Note that we have to find only real solutions, that is, we have to find only those values of x that can be represented on a number line. The numerical values that cannot be represented on the number line are known as complex numbers and include an imaginary part “iota” that is equal to $\sqrt { - 1}$ .