Question

How do you find the period of $y=2\sin x$?

Answer 1

The standard form of the sine function is $y=a\sin \left( bx+c \right)+d$, here a, b, c, and d $\in$Real numbers. For this equation, the amplitude is $\left| a \right|$, period is $\dfrac{2\pi }{b}$, phase shift is $\dfrac{-c}{b}$, and vertical shift is d. By comparing the coefficients of the equation, we can find the a, b, c, d, and thus amplitude, period, and shifts can also be found.

Complete step by step answer:
We are given the cosine function $y=2\sin x$. We have to find its amplitude, period, and shifts. The standard form of the cosine function is $y=a\sin \left( bx+c \right)+d$. Comparing the given cosine equation with standard form we get, $a=2,b=1,c=0,$ and $d=0$.
We can find the period from the values of the coefficients as follows,
For a standard sine function $y=a\sin \left( bx+c \right)+d$, the period is $\dfrac{2\pi }{b}$, substituting the values we get, period of given function as $\dfrac{2\pi }{b}=\dfrac{2\pi }{1}=2\pi$.

Hence, the period of the given sine function is $2\pi$.

Note: We can also find the amplitude, horizontal/phase shift, and vertical shift from the value of coefficients as follows,
Amplitude of given equation is $\left| a \right|=\left| 2 \right|=2$, horizontal/ phase shift of the equation is $\dfrac{-c}{b}=\dfrac{0}{1}=0$, and vertical shift of equation is d $=0$.
We can plot the graph of the given sine function using these values, as

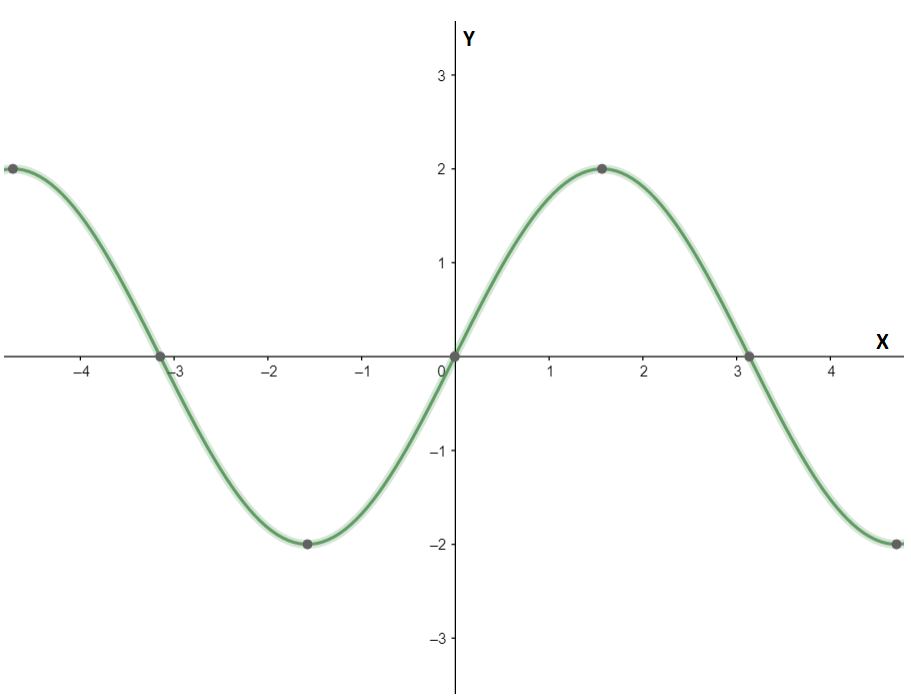
A similar type of question can be asked for cosine functions also, for that we should know what the standard form of the cosine function is: $y=a\cos \left( bx+c \right)+d$. Same as for the sine function here also a, b, c, and d $\in$Real numbers. For this equation, the amplitude is $\left| a \right|$, period is $\dfrac{2\pi }{b}$, phase shift is $\dfrac{-c}{b}$, and vertical shift is d.