Question

How do you find the period of $\tan x$?

Answer 1

We first explain the meaning of period for a given function. We draw the graph for our given function $f\left( x \right)=\tan x$. We try to find the value of the interval for which the graph goes into repetitive mode. We find the value from the graph and put that value in the equation of $f\left( x+a \right)=f\left( x \right)$. If the value satisfies that equation then the period value gets verified.

Complete step by step solution:
The period of $\tan x$ is $\pi$. To find the period we need to use the graph of the ratio.

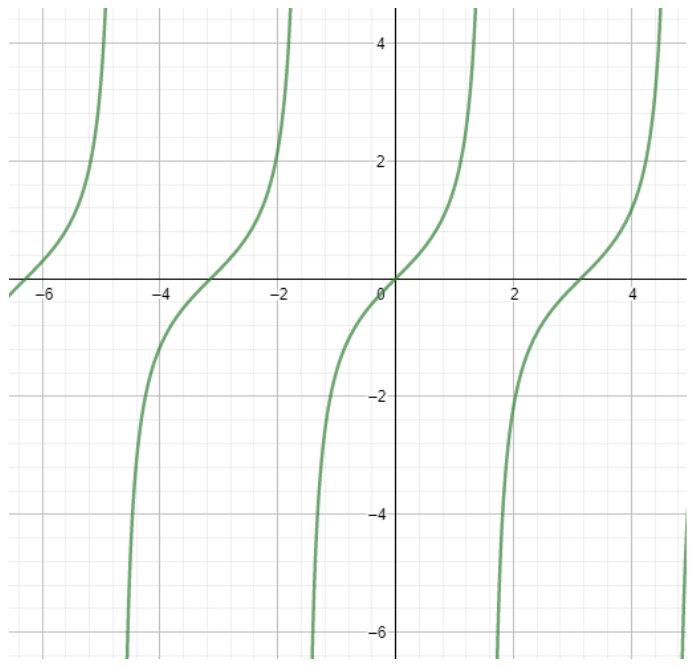
The line gets the repetition after the gap of $\pi$. The period of a function is the value on which the graph repeats its value.
If $f\left( x \right)$ be the given function then $a$ will be the period of the function when $f\left( x+a \right)=f\left( x \right)$.
We check the same for our given function $f\left( x \right)=\tan x$.
We need to find the value of $f\left( x+\pi \right)$.
Therefore, $f\left( x+\pi \right)=\tan \left( x+2\times \dfrac{\pi }{2} \right)$. The angle goes in the third quadrant which is positive for $\tan x$. Therefore, the sign of $f\left( x+\pi \right)$ remains positive. Also, we are increasing the angle in an even multiple of $\dfrac{\pi }{2}$. This means the ratio remains fixed at $\tan x$.
So, $\tan \left( x+2\times \dfrac{\pi }{2} \right)=\tan \left( x \right)$.
The value for the increase of angle $\pi$ remains the same. This proves that the period of $\tan x$ is $\pi$.

Note: Although the range of the function $f\left( x \right)=\tan x$ is $\left( -\infty ,\infty \right)$. The period of the function remains $\pi$ for $\tan x,\forall x\in \mathbb{R}$. The primary domain for the function is $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$.