Question

How do you find the period of sinx?

Answer 1

Here in this question, we need to graph the function of sinx. With the help of that, we will be able to find all the values lying in the period of sinx. It will help you to find the trigonometric ratios for different angles of sine. Sine is the basic function of trigonometry, so it will also help in finding the values of derived functions.

Complete step by step answer:
Let’s discuss the most important function of trigonometry.
As we are all aware that sine is the basic function of the trigonometry. Apart from sine, cosine is also the one which contributes in deriving other functions. When we say sin$\theta$, here $\theta$ represents angle in either degrees or in radians.
In the above triangle, $\theta$ is the angle at C. So,
sin$\theta$ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
Functions which are derived from basic functions are:
$\Rightarrow$cosec$\theta$ = $\dfrac{1}{\sin \theta }$
$\Rightarrow$sec$\theta$ = $\dfrac{1}{\cos \theta }$
$\Rightarrow$tan$\theta$ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow$cot$\theta$ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Now, let’s make a table of trigonometric ratios for all the trigonometric functions i.e. sin, cos, tan, cot, sec and cosec.

Trigonometric ratios(angle $\theta$ in degrees)	${{0}^{\circ }}$	${{30}^{\circ }}$	${{45}^{\circ }}$	${{60}^{\circ }}$	${{90}^{\circ }}$
sin$\theta$	0	$\dfrac{1}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{\sqrt{3}}{2}$	1
cos$\theta$	1	$\dfrac{\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{2}$	0
tan$\theta$	0	$\dfrac{1}{\sqrt{3}}$	1	$\sqrt{3}$	$\infty$
cosec$\theta$	$\infty$	2	$\sqrt{2}$	$\dfrac{2}{\sqrt{3}}$	1
sec$\theta$	1	$\dfrac{2}{\sqrt{3}}$	$\sqrt{2}$	2	$\infty$
cot$\theta$	$\infty$	$\sqrt{3}$	1	$\dfrac{1}{\sqrt{3}}$	0

Period of sinx is $2\pi$. Let’s see its graphical representation.

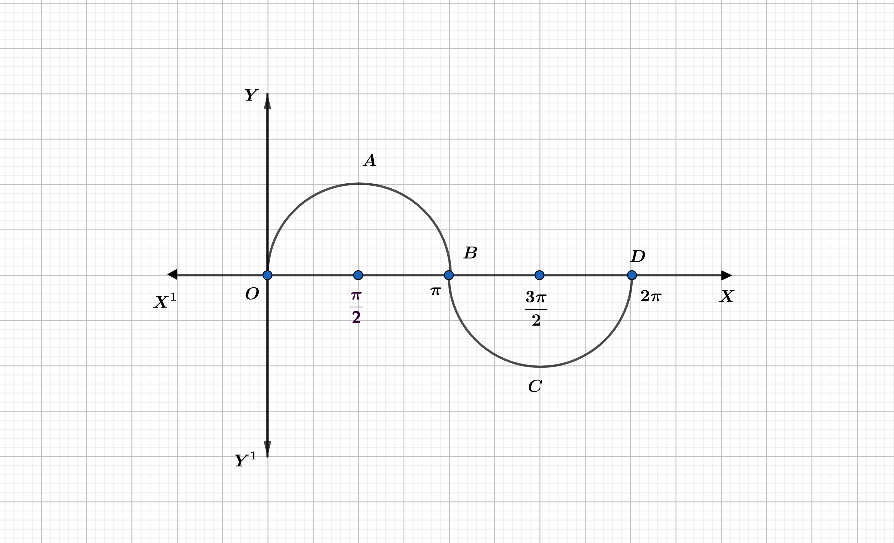
From the graph, we can see that sinx completes one full cycle of ${{360}^{\circ }}$ i.e. $2\pi$.

Note:
For every even angle formed of sine like $2\pi$, $4\pi$, $6\pi$ and so on, the value will be 0. Sine is a periodic function. It has a fixed interval of $2\pi$. It completes its half cycle at $\pi$ i.e. ${{180}^{\circ }}$. Trigonometric tables are used to find trigonometric ratios at different angles formed in the graph. If we plot all the trigonometric ratios on the graph till $2\pi$, we will get the same curve.