Question

How do you find the period and graph the function $y = 4\tan x$?

Answer 1

We know that the distance between the repetitions of any function is called the period of the function.
For a trigonometric function, the length of one complete cycle is called a period.
If we have a function ${\text{f}}\left( {\text{a}} \right) = {\text{tan}}\left( {{\text{as}}} \right)$, where $s > 0$, then the graph of the function makes complete cycles between $- \dfrac{\pi }{2},0$ and $0,\dfrac{\pi }{2}$ each of the function have the period of $p = \dfrac{\pi }{s}$
Substitute the value of $s$, we can find the period.

Complete step-by-step solution:
It is given that; $y = 4\tan x$
We have to find the period and graph of the given function.
We know that the distance between the repetitions of any function is called the period of the function. For a trigonometric function, the length of one complete cycle is called a period.
If we have a function${\text{f}}\left( {\text{a}} \right){\text{ }} = {\text{ tan}}\left( {{\text{as}}} \right)$, where$s > 0$, then the graph of the function makes complete cycles between $- \dfrac{\pi }{2},0$ and $0,\dfrac{\pi }{2}$ each of the function have the period of $p = \dfrac{\pi }{s}$
Here, $s = 4$
So, the period of the given function $y = 4\tan x$ is $\dfrac{\pi }{4}$.
Answer, here’s the graph of $y = 4\tan x$

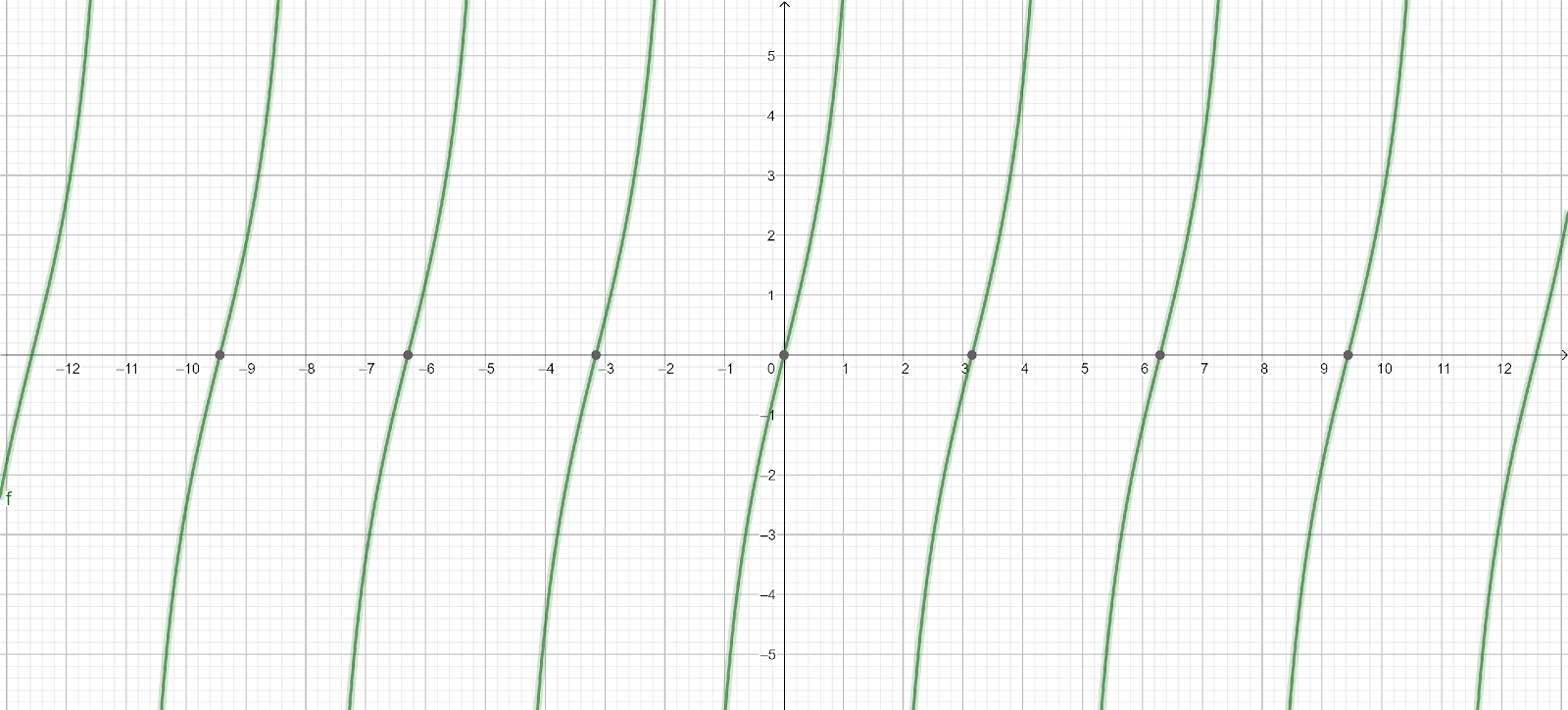
Note: The time interval between two waves is known as a Period whereas a function that repeats its values at regular intervals or periods is known as a Periodic Function. In other words, a periodic function is a function that repeats its values after every particular interval.
If a function repeats over at a constant period, we say that is a periodic function.
It is represented like $f(x) = f(x + p)$, p is the real number and this is the period of the function.
Period means the time interval between the two occurrences of the wave.