Question

How do you find the parametric equations for the line through the point ( 0, 1, 2) that is perpendicular to the line x =1 + t , y=1 – t, z= 2t and intersect the line ?

Answer 1

First we will take the intersecting point as a parametric form, we know that the point of intersection will lie on the given line. We can find the vector of a line by using 2 points on the line. If we know the vector and a point on a line we can easily find the equation of the line.

Complete step by step solution:
The equation of the given line $x =1 + t , y=1 – t, z= 2t$ , we need to find the equation of line which passes through the given line and perpendicular to it and it also passes through (0, 1, 2)
Let’s take the parametric point on the given line by which the perpendicular line passes as $\left( 1+t , 1 – t, 2t \right)$
We know that if 2 vectors are perpendicular then the dot product will be 0
The perpendicular line passes through $\left( 1+t , 1 – t, 2t \right)$ and $\left(0, 1, 2 \right)$, so the vector of the line $\left( 1+t \right)\overset{\hat{\ }}{\mathop{i}}\,-t\overset{\hat{\ }}{\mathop{j}}\,+\left( 2t-2 \right)\overset{\hat{\ }}{\mathop{k}}\,$
The dot product is 0 so we can write $\left( \left( 1+t \right)\overset{\hat{\ }}{\mathop{i}}\,-t\overset{\hat{\ }}{\mathop{j}}\,+\left( 2t-2 \right)\overset{\hat{\ }}{\mathop{k}}\, \right).\left( \overset{\hat{\ }}{\mathop{i}}\,-\overset{\hat{\ }}{\mathop{j}}\,+2\overset{\hat{\ }}{\mathop{k}}\, \right)$ which is $6t – 3 = 0$
So t is equal to $0.5$ and the vector is We know the vector of the line is $\left( 1+t \right)\overset{\hat{\ }}{\mathop{i}}\,-t\overset{\hat{\ }}{\mathop{j}}\,+\left( 2t-2 \right)\overset{\hat{\ }}{\mathop{k}}\,$
So we put $t = 0.5$ in the above equation we get the vector of the line is equal to $1.5\overset{\hat{\ }}{\mathop{i}}\,-0.5\overset{\hat{\ }}{\mathop{j}}\,-1\overset{\hat{\ }}{\mathop{k}}\,$
If we double it and write $3\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,-2\overset{\hat{\ }}{\mathop{k}}\,$
So the parametric form of the equation is $t \left( 3\overset{\hat{\ }}{\mathop{i}}\,-1\overset{\hat{\ }}{\mathop{j}}\,-2\overset{\hat{\ }}{\mathop{k}}\, \right)$ + $\left(0, 1, 2 \right)$ so the equation of the line $x = 3 t , y = 1 – t \text{ and } z = 2 - 2t$
Let’s draw the figure of the line

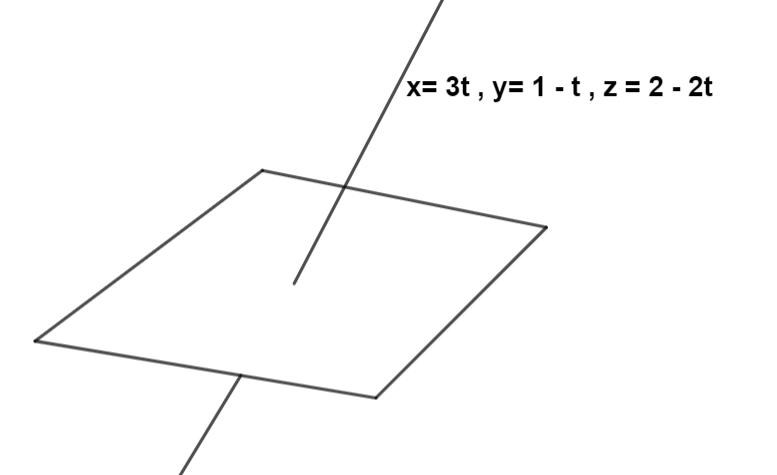
Note: In one case we can find the equation of perpendicular line if the point (0, 1, 2) lies on the given line, in that case there will be no possible line that passes through the point and intersects by right angle. Always remember if 2 vectors are perpendicular then their dot product is always 0.