Question

How do you find the missing side of the right triangle with legs: $a = 5$, $b = 12$?

Answer 1

Here, we are given the dimensions of two legs of the right angle triangle. Therefore, it is obvious that the missing side is the hypotenuse which is the longest sie of the triangle opposite to the right angle. For finding our answer, we will use the Pythagoras law.

Complete step-by-step solution:
We are given the legs of the right angle triangle as $a = 5$ and $b = 12$.
Let the missing side which is hypotenuse is $c$.

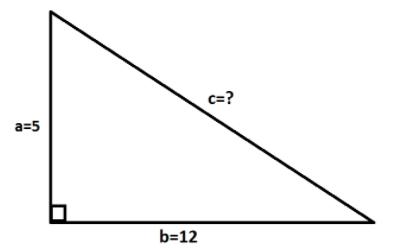
We know that the Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
Therefore, if we apply the Pythagoras theorem in our case, we get
${c^2} = {a^2} + {b^2}$
We are given that $a = 5$ and $b = 12$.
$\Rightarrow {c^2} = {5^2} + {12^2} \\\ \Rightarrow {c^2} = 25 + 144 \\\ \Rightarrow {c^2} = 169 \\\ \Rightarrow c = 13 \\\$
Thus, the value of the missing side in the right angle triangle is $13$.

Note: We have used the Pythagoras theorem to solve this question. There is another theorem which is called the inverse of Pythagoras theorem. The inverse of the Pythagorean Theorem is: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. Also, The Pythagorean Theorem is useful for two-dimensional navigation. We can use it and two lengths to find the shortest distance, the distances north and west will be the two legs of the triangle, and the shortest line connecting them will be the diagonal.