Question

How do you find the minimum and maximum value of $y = - {\left( {x - 3} \right)^2} - 4$?

Answer 1

Here, we need to find the minimum and maximum value of the given function. First, we will find the first derivative of the function. Then, we will find the points at which the first derivative is equal to 0. Finally, we will use the second derivative test to check which point is the point of maximum and minimum value and substitute the coordinate in the function to find the maximum and minimum value.

Formula Used:
We will use the following formulas:
1. $\dfrac{{d\left( {u + v} \right)}}{{dx}} = \dfrac{{d\left( u \right)}}{{dx}} + \dfrac{{d\left( v \right)}}{{dx}}$
2. The derivative of a function of the form $a{\left[ {f\left( x \right)} \right]^n}$ is given by $na{\left[ {f\left( x \right)} \right]^{n - 1}} \times \dfrac{{d\left[ {f\left( x \right)} \right]}}{{dx}}$.
3. $\dfrac{{d\left( {ax} \right)}}{{dx}} = a$

Complete step-by-step solution:
First, we will find the first derivative of the given function.
Differentiating both sides of the given equation, we get
$\dfrac{{dy}}{{dx}} = \dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2} - 4} \right]}}{{dx}}$
The derivative of the sum of two functions can be written as the sum of the derivatives of the individual functions. This can be written as $\dfrac{{d\left( {u + v} \right)}}{{dx}} = \dfrac{{d\left( u \right)}}{{dx}} + \dfrac{{d\left( v \right)}}{{dx}}$.
Using the sum of derivatives, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2}} \right]}}{{dx}} + \dfrac{{d\left[ { - 4} \right]}}{{dx}}$
The derivative of a constant is always 0.
Therefore, we get
$\dfrac{{d\left[ { - 4} \right]}}{{dx}} = 0$
Substituting $\dfrac{{d\left[ { - 4} \right]}}{{dx}} = 0$ in the equation, we get
$\begin{array}{l} \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2}} \right]}}{{dx}} + 0\\\ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2}} \right]}}{{dx}}\end{array}$
The derivative of a function of the form $a{\left[ {f\left( x \right)} \right]^n}$ is given by $na{\left[ {f\left( x \right)} \right]^{n - 1}} \times \dfrac{{d\left[ {f\left( x \right)} \right]}}{{dx}}$.
Therefore, we get the derivative of the function $- {\left( {x - 3} \right)^2}$ as
$\dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2}} \right]}}{{dx}} = - 2{\left( {x - 3} \right)^{2 - 1}} \times \dfrac{{d\left( {x - 3} \right)}}{{dx}}$
Substituting $\dfrac{{d\left[ { - {{\left( {x - 3} \right)}^2}} \right]}}{{dx}} = - 2{\left( {x - 3} \right)^{2 - 1}} \times \dfrac{{d\left( {x - 3} \right)}}{{dx}}$ in the equation, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2{\left( {x - 3} \right)^{2 - 1}} \times \dfrac{{d\left( {x - 3} \right)}}{{dx}}$
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow \dfrac{{dy}}{{dx}} = - 2{\left( {x - 3} \right)^1} \times \dfrac{{d\left( {x - 3} \right)}}{{dx}}\\\ \Rightarrow \dfrac{{dy}}{{dx}} = - 2\left( {x - 3} \right) \times \dfrac{{d\left( {x - 3} \right)}}{{dx}}\end{array}$
Using the sum of derivatives, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2\left( {x - 3} \right) \times \left[ {\dfrac{{d\left( x \right)}}{{dx}} + \dfrac{{d\left( { - 3} \right)}}{{dx}}} \right]$
The value of the derivative of a constant is always 0.
The value of a variable with respect to itself is always 1.
Therefore, the equation becomes
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2\left( {x - 3} \right) \times \left[ {1 + 0} \right]$
Adding the terms, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2\left( {x - 3} \right) \times 1$
Multiplying the terms, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2\left( {x - 3} \right)$
Multiplying the terms using the distributive law of multiplication, we get
$\Rightarrow \dfrac{{dy}}{{dx}} = - 2x + 6$
This is the value of the first derivative.
We will equate the first derivative to 0.
Equating the first derivative to 0, we get
$\Rightarrow - 2x + 6 = 0$
This is a linear equation in terms of $x$. We will solve it to find the value of $x$, and hence, the point of local maxima/minima.
Adding $2x$ on both sides of the equation, we get
$\Rightarrow 6 = 2x$
Dividing both sides of the equation by 2, we get
$\Rightarrow 3 = x$
Now, we will find the second derivative of the function by differentiating the first derivative.
If the second derivative is greater than 0, then the point $x = 3$ is the point of minimum value.
If the second derivative is lesser than 0, then the point $x = 3$ is the point of maximum value.
Differentiating both sides of the equation $\dfrac{{dy}}{{dx}} = - 2x + 6$, we get
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = \dfrac{{d\left( { - 2x + 6} \right)}}{{dx}}$
Using the sum of derivatives, we get
$\Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = \dfrac{{d\left( { - 2x} \right)}}{{dx}} + \dfrac{{d\left( 6 \right)}}{{dx}}$
The derivative of the product of a constant and a variable, with respect to that variable, is equal to the constant, that is $\dfrac{{d\left( {ax} \right)}}{{dx}} = a$.
Therefore, we get
$\begin{array}{l} \Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = - 2 + 0\\\ \Rightarrow \dfrac{{{d^2}y}}{{d{x^2}}} = - 2\end{array}$
The second derivative is less than 0.
Therefore, the point $x = 3$ is the point of maximum value.
Substituting $x = 3$ in the given equation, we get
$\Rightarrow y = - {\left( {3 - 3} \right)^2} - 4$
Subtracting 3 from 3, we get
$\begin{array}{l} \Rightarrow y = - {\left( 0 \right)^2} - 4\\\ \Rightarrow y = - 0 - 4\\\ \Rightarrow y = - 4\end{array}$

Therefore, the maximum value of the given function is $- 4$. The function has no minimum value.

Note:
We have used the distributive law of multiplication in the solution. The distributive law of multiplication states that $a \cdot b + a \cdot c = a\left( {b + c} \right)$.
Verification: We can verify the maximum value by drawing the graph of the given equation.
Drawing the graph of $y = - {\left( {x - 3} \right)^2} - 4$, we get

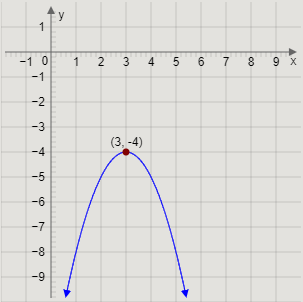
We can observe that the graph of the equation $y = - {\left( {x - 3} \right)^2} - 4$ has maximum value as $- 4$, and has no minimum value.