Solveeit Logo
Login

Question

Question: How do you find the midpoint of \(\left( 5,-2 \right)\), \(\left( 3,-6 \right)\)?...

How do you find the midpoint of (5,−2)\left( 5,-2 \right), (3,−6)\left( 3,-6 \right)?

Explanation

Solution

In this question we have been given with two points which make up a line. We have to find the midpoint of the line which is the point which is equidistant from both the points or which is in the exact middle of the line segment. We will use the midpoint formula which is M=(x1+x22,y1+y22)M=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right), where MM is the midpoint in the form (x,y)\left( x,y \right), (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) are the coordinates of the first point and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) are the coordinates of the second point. We will also plot the graph for the line and the midpoint.

Complete step by step solution:
We have the given points as (5,−2)\left( 5,-2 \right) and (3,−6)\left( 3,-6 \right).
We will consider (x1,y1)=(5,−2)\left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,-2 \right) and (x2,y2)=(3,−6)\left( {{x}_{2}},{{y}_{2}} \right)=\left( 3,-6 \right).
On making a line using the two coordinates, we get:

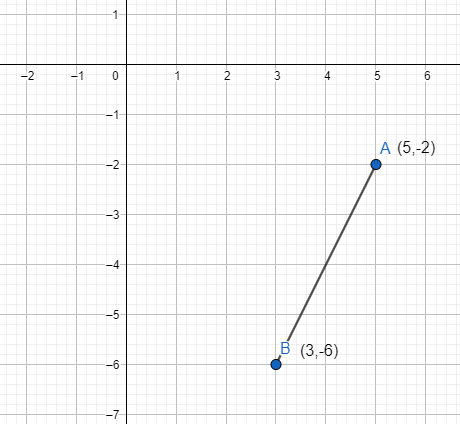
Now we know the midpoint formula: M=(x1+x22,y1+y22)M=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)
On substituting the values in the formula, we get:
⇒M=(5+32,−2+(−6)2)\Rightarrow M=\left( \dfrac{5+3}{2},\dfrac{-2+\left( -6 \right)}{2} \right)
On simplifying the brackets, we get:
⇒M=(5+32,−2−62)\Rightarrow M=\left( \dfrac{5+3}{2},\dfrac{-2-6}{2} \right)
On simplifying the values, we get:
⇒M=(82,−82)\Rightarrow M=\left( \dfrac{8}{2},\dfrac{-8}{2} \right)
On dividing the points, we get:
⇒M=(4,−4)\Rightarrow M=\left( 4,-4 \right), which is the required midpoint for the given points.
On making plotting the midpoint MM on the graph, we get:

Which is the required solution.

Note: It is to be remembered that when the midpoint of any given line segment is found, the coordinate will be placed in the middle of the line segment. If the coordinate is not visually present in the middle of the line segment, then there has been some error in calculation and the answer is incorrect. In this example we can see that the midpoint is visually, in the middle of the line segment therefore, this answer is correct.