Question

How do you find the linearization of $f\left( x \right) = 4{x^3} - 5x - 1$ at $a = 2$?

Answer 1

First, substitute the value of $a = 2$ into the linearization function. Then evaluate $f\left( 2 \right)$ by replacing the variable $x$ with $2$ in the expression. Next, find the derivative of $f\left( x \right) = 4{x^3} - 5x - 1$ by differentiating $f\left( x \right)$ with respect to $x$ using differentiation properties. Next, evaluate $f'\left( 2 \right)$ by replacing the variable $x$ with $2$ in the expression. Next, substitute the components into the linearization function in order to find the linearization at $a$. Then, we will get the linearization of $f\left( x \right) = 4{x^3} - 5x - 1$ at $a = 2$.

Formula used:

1. The differentiation of the product of a constant and a function = the constant $\times$ differentiation of the function.
   i.e., $\dfrac{d}{{dx}}\left( {kf\left( x \right)} \right) = k\dfrac{d}{{dx}}\left( {f\left( x \right)} \right)$, where $k$ is a constant.
2. The differentiation of the sum or difference of a finite number of functions is equal to the sum or difference of the differentiation of the various functions.
   i.e., $\dfrac{d}{{dx}}\left[ {f\left( x \right) \pm g\left( x \right)} \right] = \dfrac{d}{{dx}}f\left( x \right) \pm \dfrac{d}{{dx}}g\left( x \right)$
3. Differentiation formula: $\dfrac{{d{x^n}}}{{dx}} = n{x^{n - 1}},n \ne - 1$

Complete step by step solution:
Given function: $f\left( x \right) = 4{x^3} - 5x - 1$
Now, consider the function used to find the linearization at $a$.
$L\left( x \right) = f\left( a \right) + f'\left( a \right)\left( {x - a} \right)$
Now, substitute the value of $a = 2$ into the linearization function.
$L\left( x \right) = f\left( 2 \right) + f'\left( 2 \right)\left( {x - 2} \right)$
Now, we have to evaluate $f\left( 2 \right)$.
For this replace the variable $x$ with $2$ in the expression.
$f\left( 2 \right) = 4{\left( 2 \right)^3} - 5\left( 2 \right) - 1$
$\Rightarrow f\left( 2 \right) = 4\left( 8 \right) - 10 - 1$
$\Rightarrow f\left( 2 \right) = 32 - 11$
$\Rightarrow f\left( 2 \right) = 21$
Now, find the derivative and evaluate it at $a = 2$.
So, we have to first find the derivative of $f\left( x \right) = 4{x^3} - 5x - 1$.
Differentiate $f\left( x \right)$ with respect to $x$.
$f'\left( x \right) = \dfrac{d}{{dx}}\left( {4{x^3} - 5x - 1} \right)$…(i)
Now, using the property that the differentiation of the sum or difference of a finite number of functions is equal to the sum or difference of the differentiation of the various functions.
i.e., $\dfrac{d}{{dx}}\left[ {f\left( x \right) \pm g\left( x \right)} \right] = \dfrac{d}{{dx}}f\left( x \right) \pm \dfrac{d}{{dx}}g\left( x \right)$
So, in differentiation (i), we can use above property
$\Rightarrow f'\left( x \right) = \dfrac{d}{{dx}}\left( {4{x^3}} \right) - \dfrac{d}{{dx}}\left( {5x} \right) - \dfrac{d}{{dx}}\left( 1 \right)$…(ii)
Now, using the property that the differentiation of the product of a constant and a function = the constant $\times$ differentiation of the function.
i.e., $\dfrac{d}{{dx}}\left( {kf\left( x \right)} \right) = k\dfrac{d}{{dx}}\left( {f\left( x \right)} \right)$, where $k$ is a constant.
So, in differentiation (ii), constants can be taken outside the differentiation.
$\Rightarrow f'\left( x \right) = 4\dfrac{d}{{dx}}\left( {{x^3}} \right) - 5\dfrac{d}{{dx}}\left( x \right) - \dfrac{d}{{dx}}\left( 1 \right)$…(iii)
Now, using the differentiation formula $\dfrac{{d{x^n}}}{{dx}} = n{x^{n - 1}},n \ne - 1$ in differentiation (iii), we get
$\Rightarrow f'\left( x \right) = 12{x^2} - 5$
Now, replace the variable $x$ with $2$ in the expression.
$f'\left( 2 \right) = 12{\left( 2 \right)^2} - 5$
$\Rightarrow f'\left( 2 \right) = 12\left( 4 \right) - 5$
$\Rightarrow f'\left( 2 \right) = 48 - 5$
$\Rightarrow f'\left( 2 \right) = 43$
Now, substitute the components into the linearization function in order to find the linearization at $a$.
$L\left( x \right) = 21 + 43\left( {x - 2} \right)$
Now, apply the distributive property.
$\Rightarrow L\left( x \right) = 21 + 43x - 86$
$\Rightarrow L\left( x \right) = 43x - 65$

Final solution: Hence, the linearization of $f\left( x \right) = 4{x^3} - 5x - 1$ at $a = 2$ is $L\left( x \right) = 43x - 65$.

Note:
We can check whether $L\left( x \right) = 43x - 65$ is the linearization of a given function, $f\left( x \right) = 4{x^3} - 5x - 1$ by plotting both functions and on graph paper.

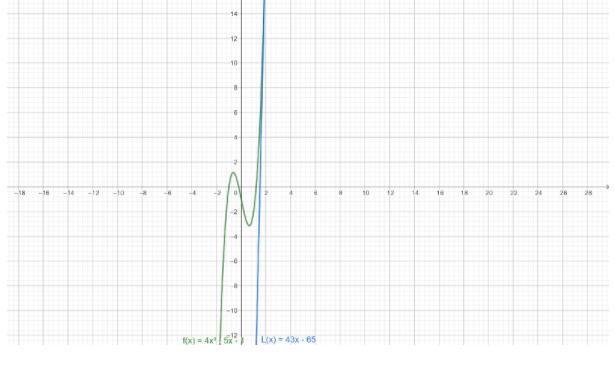
From the graph paper, we can conclude that the linearization of $f\left( x \right) = 4{x^3} - 5x - 1$ at $a = 2$ is $L\left( x \right) = 43x - 65$.
Final solution: Hence, the linearization of $f\left( x \right) = 4{x^3} - 5x - 1$ at $a = 2$ is $L\left( x \right) = 43x - 65$.