Question

How do you find the limit of $\dfrac{\left| x+2 \right|}{x+2}$ as $x$ approaches $-2$?

Answer 1

In this problem we need to calculate the limit value of the given function at given $x$ value. For this we will first check whether the given function exists at the limit value or not at a given $x$ value. So, we will first calculate the limit from the left at given $x$ value and the limit from the right at given $x$ value. For this we will write first define the given function by using the known function definition \left| x \right|=\left\\{ \begin{matrix} x,\text{ if }x\ge 0 \\\ -x,\text{ if }x<0 \\\ \end{matrix} \right.. We will this function definition to define the function $\left| x+2 \right|$. After defining the function, we will calculate the right-hand limit and left-hand limit and then we will conclude the problem by comparing both the values.

Complete step-by-step solution:
Given function, $\dfrac{\left| x+2 \right|}{x+2}$.
We know that the value of the function $\left| x \right|$ is
\left| x \right|=\left\\{ \begin{matrix} x,\text{ if }x\ge 0 \\\ -x,\text{ if }x<0 \\\ \end{matrix} \right.
From the above definition, the value of the function $\left| x+2 \right|$ will be
\left| x+2 \right|=\left\\{ \begin{matrix} x+2,\text{ if }x\ge -2 \\\ -\left( x+2 \right),\text{ if }x<-2 \\\ \end{matrix} \right.
Given that $x$ approaches $-2$.
Calculating the left-hand side limit or limit from the left-hand side.
Left hand side limit means the value of $x$ is less than $-2$ i.e., $x<-2$.
If $x<-2$ the value of the function $\left| x+2 \right|$ is
$\left| x+2 \right|=-\left( x+2 \right)$
From the above value the value of the given function $\dfrac{\left| x+2 \right|}{x+2}$ will be
$\begin{aligned} & \dfrac{\left| x+2 \right|}{x+2}=\dfrac{-\left( x+2 \right)}{x+2} \\\ & \Rightarrow \dfrac{\left| x+2 \right|}{x+2}=-1 \\\ \end{aligned}$
Applying the left-hand limit to the given function, then we will get
$\begin{aligned} & \displaystyle \lim_{x \to -{{2}^{-}}}\dfrac{\left| x+2 \right|}{x+2}=\displaystyle \lim_{x \to -{{2}^{-}}}-1 \\\ & \Rightarrow \displaystyle \lim_{x \to -{{2}^{-}}}\dfrac{\left| x+2 \right|}{x+2}=-1 \\\ \end{aligned}$
Calculating the right-hand limit or limit from the right hand side.
Right hand side limit means $x>-2$.
If $x>-2$ the value of the function $\left| x+2 \right|$ is
$\left| x+2 \right|=x+2$
From the above value the value of the given function $\dfrac{\left| x+2 \right|}{x+2}$ will be
$\begin{aligned} & \dfrac{\left| x+2 \right|}{x+2}=\dfrac{x+2}{x+2} \\\ & \Rightarrow \dfrac{\left| x+2 \right|}{x+2}=1 \\\ \end{aligned}$
Applying the right-hand limit to the given function, then we will get
$\begin{aligned} & \displaystyle \lim_{x \to -{{2}^{+}}}\dfrac{\left| x+2 \right|}{x+2}=\displaystyle \lim_{x \to -{{2}^{+}}}1 \\\ & \Rightarrow \displaystyle \lim_{x \to -{{2}^{+}}}\dfrac{\left| x+2 \right|}{x+2}=1 \\\ \end{aligned}$
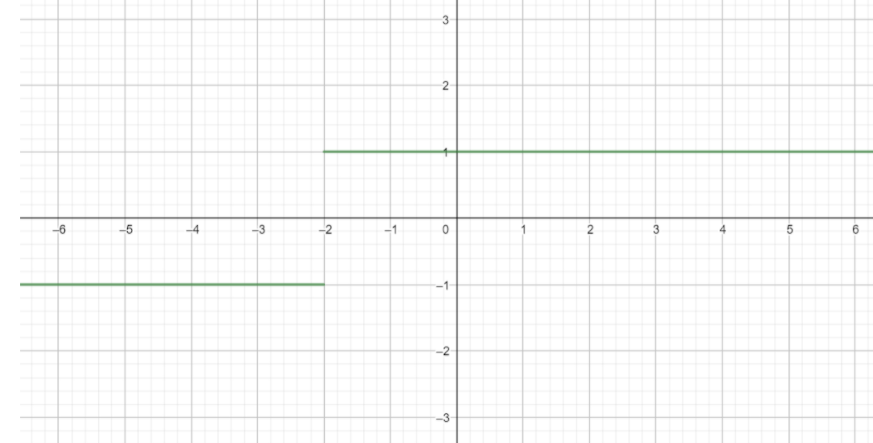
Here we have $\displaystyle \lim_{x \to -{{2}^{+}}}\dfrac{\left| x+2 \right|}{x+2}\ne \displaystyle \lim_{x \to -{{2}^{-}}}\dfrac{\left| x+2 \right|}{x+2}$. So, the limit of the function doesn’t exist.

Note: We can clearly observe that the function is simply $y=1$ for $x>-2$ and $y=-1$ for $x<-2$. So, we can’t calculate the limit of the function. We can also observe this in the graph of the given equation which is shown in below figure