Question

How do you find the limit of $\dfrac{{2 - {e^x}}}{{2 + 3{e^x}}}$ as $x$ approaches to infinity?

Answer 1

Hint : In order to determine the limit of the above function, replace all the ${e^x}$ with ${e^{ - x}}$ in the expression by multiplying and dividing the limit with ${e^{ - x}}$ in order to obtain a consistent result as when $x \to \infty$ then ${e^{ - x}} \to 0$ . With the use of exponent law , simplify the limit and put the result ${e^{ - x}} \to 0$ when $x \to \infty$ to obtain the required result.

Complete step by step solution:
We are given a exponential function in variable $x$ i.e. $\dfrac{{2 - {e^x}}}{{2 + 3{e^x}}}$ having limit $x \to \infty$ .
$\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}}$
To better understand and calculate the limits of the above expression, let's look into the graph of the $y = \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}}$ .

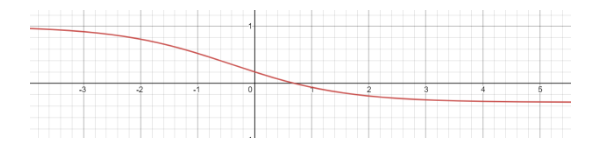
As we can clearly see that the if the limit for $x \to \infty$, then ${e^x} \to \infty$ which will make the function inconsistent but one the other side we can see is $x \to \infty$ then ${e^{ - x}} \to 0$
So it's better to replace the ${e^x}$ with ${e^{ - x}}$ in the expression to get the result of the limit completely in the consistent form.
And to do so , we will be multiplying and dividing the limit expression with ${e^{ - x}}$ , rewriting the limit function as

$$\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} \times \dfrac{{{e^{ - x}}}}{{{e^{ - x}}}} \\\ \therefore \mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{{e^{ - x}}\left( {2 - {e^x}} \right)}}{{{e^{ - x}}\left( {2 + 3{e^x}} \right)}} \;$$

Using the distributive law of multiplication to expand and multiply the terms as $A\left( {B + C} \right) = AB + AC$ , we can rewrite the limit as
$\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{2{e^{ - x}} - {e^{ - x}}.{e^x}}}{{2{e^{ - x}} + 3{e^{ - x}}.{e^x}}}$
Using the exponent law to simplify the above expression as ${a^m} \times {a^n} = {a^{m + n}}$ . We get
$\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{2{e^{ - x}} - 1}}{{2{e^{ - x}} + 3}}$
Now using the result ${e^x} \to 0$ as $x \to \infty$ , we have

$$\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{2\left( 0 \right) - 1}}{{2\left( 0 \right) + 3}} \\\ \therefore \mathop {\lim }\limits_{x \to \infty } \dfrac{{2 - {e^x}}}{{2 + 3{e^x}}} = - \dfrac{1}{3} \;$$

Hence the above result is completely inconsistent.
Therefore the limit of $\dfrac{{2 - {e^x}}}{{2 + 3{e^x}}}$ as $x \to \infty$ is equal to $- \dfrac{1}{3}$.
So, the correct answer is “ $- \dfrac{1}{3}$”.

Note : 1. Don’t forget to cross-check your answer.
2.After putting the Limit the result should never in the indeterminate form $\dfrac{0}{0}\,or\,\dfrac{{ \pm \infty }}{{ \pm \infty }}$ . If it is contained, apply some operation to modify the result or use the L-Hospitals rule .
3. $e$ is the exponential constant having value equal to $2.71828$
4.Avoid any step jump in such types of questions as this might increase the chances of mistakes.
5. While expanding the terms, use the proper sign with the terms.