Question

How do you find the length of the polar curve $r={{\cos }^{3}}\left( \dfrac{\theta }{3} \right)$ ?

Answer 1

To find the length of polar curve $r={{\cos }^{3}}\left( \dfrac{\theta }{3} \right)$ . First of all we have to differentiate the curve and then by observing the graph we have to find out the limits and equations to get the length of the polar curve. Now, we have to differentiate the equation with the limits we found to get the length.

Complete step by step answer:
For the given problem, we are given to solve the length of the polar curve $r={{\cos }^{3}}\left( \dfrac{\theta }{3} \right)$ .
Let us consider the equation as equation (1).
$r={{\cos }^{3}}\left( \dfrac{\theta }{3} \right)........\left( 1 \right)$
Differentiation of equation (1) with respect to $\theta$ is
As we know chain rule i.e. ${{F}^{'}}\left( x \right)={{f}^{'}}\left( g\left( x \right) \right).g'\left( x \right)$ .
By applying the chain rule to equation (1), we get
$\Rightarrow \dfrac{dr}{d\theta }=3{{\cos }^{2}}\left( \dfrac{\theta }{3} \right).\left[ -\sin \left( \dfrac{\theta }{33} \right) \right].\dfrac{1}{3}$
By cleaning up a bit,
$\Rightarrow \dfrac{dr}{d\theta }=-{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)\sin \left( \dfrac{\theta }{3} \right)$
Let us consider the above equation as equation (2)
$\Rightarrow \dfrac{dr}{d\theta }=-{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)\sin \left( \dfrac{\theta }{3} \right).......\left( 2 \right)$
Let us look at the graph of curve $r={{\cos }^{3}}\dfrac{\theta }{3}$ which looks like

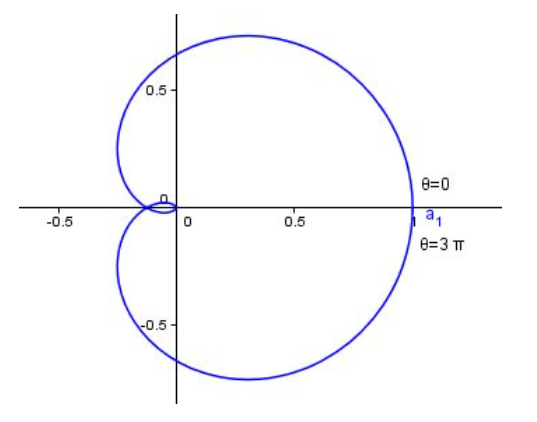
We can clearly say that $\theta$ goes from $0$ to $3\pi$ to complete the loop once.
Let us find the length L of the curve.
$L=\int\limits_{0}^{3\pi }{\sqrt{{{r}^{2}}+{{\left( \dfrac{dr}{d\theta } \right)}^{2}}d\theta }}$
By simplifying we will get,
$=\int\limits_{0}^{3\pi }{\sqrt{{{\cos }^{6}}\left( \dfrac{\theta }{3} \right)+{{\cos }^{4}}\left( \dfrac{\theta }{3} \right){{\sin }^{2}}\left( \dfrac{\theta }{3} \right)d\theta }}$
Let us consider the above equation as equation (3)
$L=\int\limits_{0}^{3\pi }{\sqrt{{{\cos }^{6}}\left( \dfrac{\theta }{3} \right)+{{\cos }^{4}}\left( \dfrac{\theta }{3} \right){{\sin }^{2}}\left( \dfrac{\theta }{3} \right)d\theta }}.......\left( 3 \right)$
By pulling ${{\cos }^{2}}\left( \dfrac{\theta }{3} \right)$ from equation (3) we get
$\Rightarrow L=\int\limits_{0}^{3\pi }{{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)}\sqrt{{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)+{{\sin }^{2}}\left( \dfrac{\theta }{3} \right)d\theta }$
Let us consider the above equation as equation (4)
$L=\int\limits_{0}^{3\pi }{{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)}\sqrt{{{\cos }^{2}}\left( \dfrac{\theta }{3} \right)+{{\sin }^{2}}\left( \dfrac{\theta }{3} \right)d\theta }........\left( 4 \right)$
As we know the formulas

& {{\cos }^{2}}\theta =\dfrac{1}{2}\left( 1+\cos 2\theta \right) \\\ & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\\ \end{aligned}$$ Let us consider the formulas as formulas ($f_1$) and ($f_2$) respectively. $$\begin{aligned} & {{\cos }^{2}}\theta =\dfrac{1}{2}\left( 1+\cos 2\theta \right)..........($f_1$) \\\ & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1........($f_2$) \\\ \end{aligned}$$ By applying the formulas ($f_1$) and ($f_2$) to the equation (4) we get $$\Rightarrow L=\dfrac{1}{2}\int\limits_{0}^{3\pi }{\left( 1+\cos \left( \dfrac{2\theta }{3} \right) \right)}d\theta $$ Let us consider the above equation as equation (5). $$L=\dfrac{1}{2}\int\limits_{0}^{3\pi }{\left( 1+\cos \left( \dfrac{2\theta }{3} \right) \right)}d\theta ........(5)$$ By simplifying the equation (5) we get $$\Rightarrow L=\dfrac{1}{2}\left( \theta +\dfrac{3}{2}\sin \left( \dfrac{2\theta }{3} \right) \right)_{0}^{3\pi }$$ Let us consider the above equation as equation (6). $$L=\dfrac{1}{2}\left( \theta +\dfrac{3}{2}\sin \left( \dfrac{2\theta }{3} \right) \right)_{0}^{3\pi }.........\left( 6 \right)$$ By applying the limits to the equation we get $$\begin{aligned} & \Rightarrow L=\dfrac{1}{2}\left( 3\pi \right) \\\ & \Rightarrow L=\dfrac{3\pi }{2} \\\ \end{aligned}$$ Let us consider $$L=\dfrac{3\pi }{2}.......\left( 7 \right)$$ **So, therefore the polar length of the curve is $$L=\dfrac{3\pi }{2}$$ .** **Note:** While applying the limits to our equation we should remember that $$\int\limits_{b}^{a}{f'\left( x \right)}dx=f\left( a \right)-\left( b \right)$$ because students may confuse like $$\int\limits_{b}^{a}{f'\left( x \right)}dx=f\left( b \right)-\left( a \right)$$ . We should have good knowledge on trigonometry formulas while doing these problems because formulas will play a key role while doing this problem.