Question

How do you find the inverse of $y={{4}^{x}}$ and is it a function?

Answer 1

We know that if $y=f\left( x \right)$ then if there exists a function g such that $g\left( y \right)=x$ then we can say g and f are inverse functions of each other. We can write $f\left( x \right)={{g}^{-1}}\left( x \right),g\left( x \right)={{f}^{-1}}\left( x \right)$ and $f\left( g\left( x \right) \right)=x,g\left( f\left( x \right) \right)=x$ . We know that if ${{a}^{x}}=b$ then $x={{\log }_{a}}b$ so we use logarithm to find the inverse function of $y={{4}^{x}}$ . If $f\left( x \right)$ to be a function for every x in the domain if $f\left( x \right)=a$ and $f\left( x \right)=b$ then a must be equal to b. x can’t have 2 images.

Complete step by step answer:
Let’s find out the inverse of $y={{4}^{x}}$ . To find out the inverse we have write the value of x in term of y that mean there exist a function g such that $g\left( y \right)=x$
We can use logarithm to express x in terms of y
We know that if ${{a}^{x}}=b$ then $x={{\log }_{a}}b$
If $y={{4}^{x}}$ then $x={{\log }_{4}}y$
Now we can see that our $g\left( y \right)$ is equal to ${{\log }_{4}}y$
We know the property of logarithm ${{\log }_{a}}b=\dfrac{\ln b}{\ln a}$
So $g\left( y \right)={{\log }_{4}}y=\dfrac{\ln y}{\ln 4}$
So inverse function of ${{4}^{x}}$ is $g\left( x \right)=\dfrac{\ln x}{\ln 4}$
Now we have to check whether g is a function or not. Property of function is for every x in the domain x can’t have more than one output or image that means if $g\left( x \right)=a$ and $g\left( x \right)=b$ then a must be equal to b.
To understand in simpler terms if we draw parallel lines to the Y axis and if each line intersects the curve only at one point then it will be a function and if each line intersects more than one point it is not a function.
Let’s draw the graph

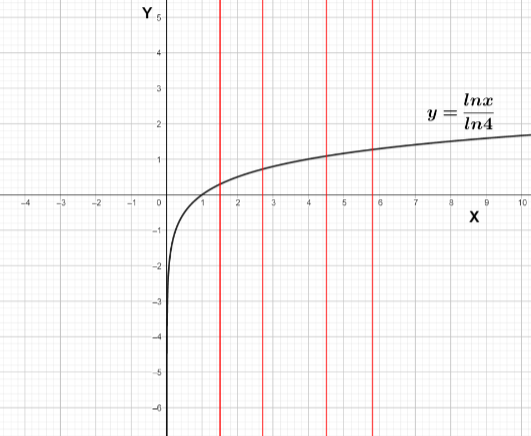
The black curve is a graph of g and red lines are parallel lines to the Y axis. We can see that they intersect at only one point so g is a function.

Note: Always keep in mind that in function every element in range can have more than one preimage but in the domain every element can’t have more than one image. To check whether a certain equation is a function or not we simply can draw the curve for the function and parallel lines to the Y axis if any of the lines intersect at more than one point it is not a function otherwise it is a function.