Question

How do you find the inverse of $f(x)=\dfrac{x+1}{x-2}$ and graph both $f$ and ${{f}^{-1}}$?

Answer 1

Any function $f$ can have its inverse function ${{f}^{-1}}$ if and only if the function $f$ is bijective. A bijective function is both one-one function and onto function. That is, each image of $f$ has a distinct preimage and the co-domain of $f$ is equal to the range of the function $f$. We find the inverse function ${{f}^{-1}}$ by considering the function $f$ to be y, expressing x in terms of y and then replacing y with x. One can verify the obtained inverse function ${{f}^{-1}}$ by an important fact that the composition of functions $f$ and ${{f}^{-1}}$ which is $f\circ {{f}^{-1}}(x)$ gives x itself.

Complete step by step answer:
In the question, the function $f$ is given as $f(x)=\dfrac{x+1}{x-2}$. Let $f(x)$ be y that is,
$f(x)=y=\dfrac{x+1}{x-2}$
Taking $\left( x\text{ }\text{ }-2 \right)$ to the left-hand side, we get
$\Rightarrow y(x-2)=x+1$
Then on expansion, we can write
$\Rightarrow yx\text{ }\text{ }-2y\text{ }=\text{ }x+1$
Rearranging the terms to simplify the equation by taking variable x as common, we get
$\Rightarrow yx\text{ }\text{ }-x\text{ }=\text{ }2y\text{ }+\text{ }1$
By taking x common, we get
$\Rightarrow x\left( y\text{ }\text{ }-1 \right)\text{ }=\text{ }2y\text{ }+\text{ }1$
Now, we write x in terms of y as
$\Rightarrow x=\dfrac{2y+1}{y-1}$
Therefore, ${{f}^{-1}}(x)=\dfrac{2x+1}{x-1}$. (on replacing y with x)

Verification: -
$f\left( {{f}^{-1}}(x) \right)=f\left( \dfrac{2x+1}{x-1} \right)=\dfrac{\dfrac{2x+1}{x-1}+1}{\dfrac{2x+1}{x-1}-2}$
$\Rightarrow \dfrac{2x+1+x-1}{2x+1-2x+2}$
$\Rightarrow 3\dfrac{x}{3}\Rightarrow x$
Hence, verified.

By substituting different values of x in $f(x)=\dfrac{x+1}{x-2}$, we get points lying on the given function. On tracing these points on the xy – plane and joining them gives an approximate graph of $f(x)=\dfrac{x+1}{x-2}$. It will same as shown in the figure below:

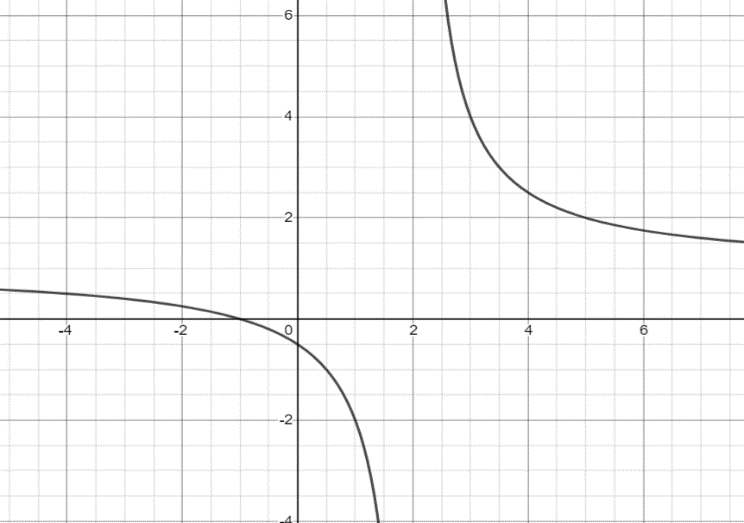
$\Rightarrow$ undefined at x=2
Similarly, we get the graph of ${{f}^{-1}}$ as shown below:

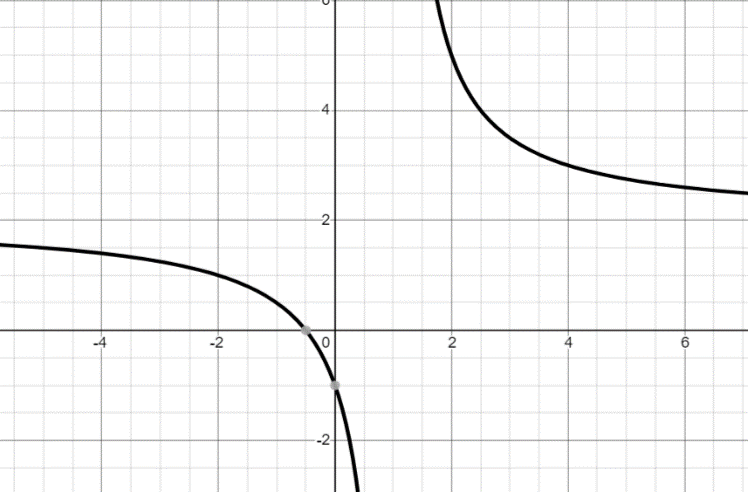
$\Rightarrow$ undefined at y=2

Note: Common errors while composing functions: Students sometimes forget where each of the functions is defined before composing functions, which lead to non – existing results. They also sometimes forget that composition is not a commutative operation that is, $f\circ g\ne g\circ f$. Also, the graphs of $f$ and ${{f}^{-1}}$ are symmetric about the line $y=x$.