Solveeit Logo
Login

Question

Question: How do you find the inverse of \(f\left( x \right)=3x-5\) and is it a function?...

How do you find the inverse of f(x)=3x−5f\left( x \right)=3x-5 and is it a function?

Explanation

Solution

To find the inverse of the given function f(x)=3x−5f\left( x \right)=3x-5, first of all, we will assume f(x)f\left( x \right) as y and write y in place of f(x)f\left( x \right) in the above function. Then, we are going to arrange this equation in such a way so that we get x in terms of y. After that, we have to check whether the inverse of the function that we have calculated is a function or not by checking the condition that only one value is possible corresponding to each x value.

Complete step-by-step answer:
The function given above which we have to find the inverse of is:
f(x)=3x−5f\left( x \right)=3x-5
Now, we are going to write y in place of f(x)f\left( x \right) in the above equation and we get,
⇒y=3x−5\Rightarrow y=3x-5
The function in x written on the R.H.S of the above equation is calculated by writing x in terms of y. For that, we are adding 5 on both the sides of the above equation we get,
⇒y+5=3x−5+5\Rightarrow y+5=3x-5+5
As you can see that 5 written on the R.H.S of the above equation will be cancelled out and we are left with:
⇒y+5=3x\Rightarrow y+5=3x
Now, dividing 3 on both the sides of the above equation we get,
⇒y+53=x\Rightarrow \dfrac{y+5}{3}=x
Now, writing x in place of y and f−1(x){{f}^{-1}}\left( x \right) in place of x in the above equation we get,
f−1(x)=x+53{{f}^{-1}}\left( x \right)=\dfrac{x+5}{3}
Hence, we have found the inverse of the above function as:
f−1(x)=x+53{{f}^{-1}}\left( x \right)=\dfrac{x+5}{3}
Now, to check whether this inverse is a function or not by taking f−1(x){{f}^{-1}}\left( x \right) as y in the above equation and then plot the following on the graph we get,
y=x+53y=\dfrac{x+5}{3}

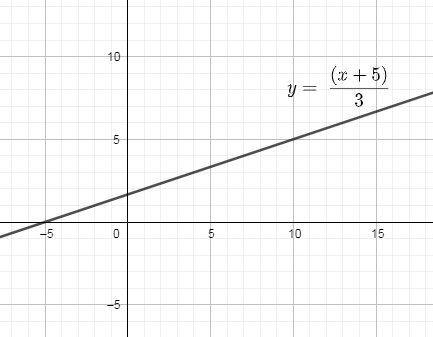
In the above graph, you can see that only one y value is possible corresponding to an x value.
So, this means that the inverse which we have calculated above is a function.

Note: The possible mistake that could be possible in the above problem is that calculation mistake when we are converting x in terms of y so be aware while converting x in terms of y.
In the above solution, we have learnt two concepts. First is, to find the inverse of any function and second is, to check whether an expression is a function or not.