Solveeit Logo
Login

Question

Question: How do you find the inverse of \(f\left( x \right)=\dfrac{2x-1}{x-1}\) and is it a function?...

How do you find the inverse of f(x)=2x−1x−1f\left( x \right)=\dfrac{2x-1}{x-1} and is it a function?

Explanation

Solution

The function given in the above problem is f(x)=2x−1x−1f\left( x \right)=\dfrac{2x-1}{x-1}. Now, let us assume this function is equal to y and then to find the inverse of this function we are going to rearrange this equation in such a way so that we get x in terms of y. After that, we have to check whether the inverse of the function that we have calculated is a function or not by seeing whether there is only one y value for an x value.

Complete step by step answer:
The function given in the above problem of which we have to find the inverse of is:
f(x)=2x−1x−1f\left( x \right)=\dfrac{2x-1}{x-1}
Now, let us equate the above function to y.
f(x)=2x−1x−1=yf\left( x \right)=\dfrac{2x-1}{x-1}=y
Inverse of the above function is calculated by writing x in terms of y. Cross multiplying the above equation we get,
2x−1x−1=y ⇒2x−1=y(x−1) ⇒2x−1=xy−y \begin{aligned} & \dfrac{2x-1}{x-1}=y \\\ & \Rightarrow 2x-1=y\left( x-1 \right) \\\ & \Rightarrow 2x-1=xy-y \\\ \end{aligned}
Subtracting xyxy on both the sides we get,
2x−xy−1=xy−xy−y ⇒2x−xy−1=−y \begin{aligned} & 2x-xy-1=xy-xy-y \\\ & \Rightarrow 2x-xy-1=-y \\\ \end{aligned}
Adding 1 on both the sides of the above equation we get,
2x−xy=−y+12x-xy=-y+1
Taking x as common from the L.H.S of the above equation we get,
x(2−y)=1−yx\left( 2-y \right)=1-y
Dividing 2−y2-y on both the sides we get,
x=1−y2−yx=\dfrac{1-y}{2-y}
Now, writing x in place of y and f−1(x){{f}^{-1}}\left( x \right) in place of x in the above equation we get,
f−1(x)=1−x2−x{{f}^{-1}}\left( x \right)=\dfrac{1-x}{2-x}
Hence, we have found the inverse of the above function as:
f−1(x)=1−x2−x{{f}^{-1}}\left( x \right)=\dfrac{1-x}{2-x}
Now, we have to check whether this inverse is a function or not. In the below, we have drawn this inverse of the given function.

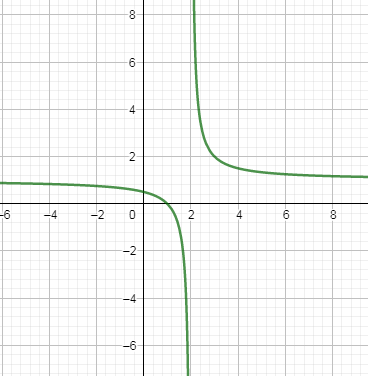
In the above graph, you can see that only one y value is possible for an x value.
So, this means that the inverse which we have calculated above is a function.

Note: In the above solution, two concepts you have learnt. First is how to find the inverse of any function and secondly, you have also learnt how to check whether an expression is a function or not.