Question

How do you find the inverse of an exponential function?

Answer 1

Here, we need to find the inverse of an exponential function. We will write the exponential function and we will assume that it is equal to $y$. Then, we will use the rule of logarithms to simplify the equation for the particular variable $x$. Then, we will interchange the variables to find the required inverse of the exponential function.

Complete step-by-step answer:
The exponential function is given by $f\left( x \right) = a{b^x}$, where $b$ is a positive real number, and $b \ne 1$.
Let $f\left( x \right)$ be equal to $y$.
Therefore, we get
$y = a{b^x}$
We will use the rule of logarithms to simplify the equation for the particular variable $x$.
First, we will isolate the exponential expression.
Dividing both sides of the equation by $a$, we get
$\Rightarrow \dfrac{y}{a} = {b^x}$
If an equation is of the form $x = {b^y}$, it can be written using logarithms as $y = {\log _b}x$, where $x > 0$, $b > 0$ and $b$ is not equal to 1.
Therefore, since $\dfrac{y}{a} = {b^x}$, we get the equation
$x = {\log _b}\left( {\dfrac{y}{a}} \right)$
Now, we will interchange the variables to find the value of the inverse of the exponential function.
Interchanging the variable $x$ and variable $y$, we get
$\Rightarrow y = {\log _b}\left( {\dfrac{x}{a}} \right)$
This is the value of the inverse of $f\left( x \right)$.
Therefore, we get
$\Rightarrow {f^{ - 1}}\left( x \right) = {\log _b}\left( {\dfrac{x}{a}} \right)$
Therefore, the inverse of an exponential function $a{b^x}$ is given by the expression ${\log _b}\left( {\dfrac{x}{a}} \right)$.

Note: We can verify the inverse by drawing the graph of an exponential function and its inverse.
Let the exponential function be $y = 2 \times {3^x}$.
We will draw the graphs of $y = 2 \times {3^x}$ and its inverse, that is $y = {\log _3}\left( {\dfrac{x}{2}} \right)$.
If the graphs are symmetrical along the line $x = y$, then the two functions are the inverse of each other.
Drawing the graphs, we get

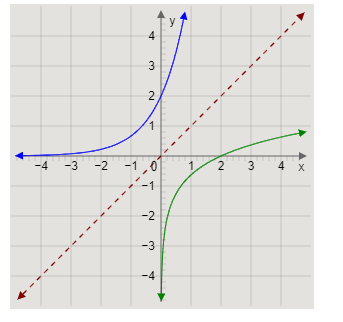
The red line is the graph of the equation $x = y$, the blue curve is the graph of the equation $y = 2 \times {3^x}$, and the green curve is the graph of the equation $y = {\log _3}\left( {\dfrac{x}{2}} \right)$.
We can observe that the graphs are symmetrical along the line $x = y$.
Therefore, we have verified that $y = 2 \times {3^x}$ is the inverse of $y = {\log _3}\left( {\dfrac{x}{2}} \right)$, and $y = {\log _3}\left( {\dfrac{x}{2}} \right)$ is the inverse of $y = 2 \times {3^x}$.