Question

How do you find the intervals on which the function is continuous given $y = \ln \left( {3x - 1} \right)$?

Answer 1

This problem deals with finding the interval of the given function which is continuous. In mathematics, a continuous function is a function that does not have any abrupt changes in value, known as discontinuities. More precisely, sufficiently small changes in the input of a continuous function result in arbitrarily small changes in its output. If not continuous, a function is said to be discontinuous.

Complete step-by-step answer:
The given function is a logarithmic function, we know that any logarithmic function of domain $x$, has the domain $x > 0$.
$\ln x$, here $x > 0$, the value of $x$ should be greater than zero, only then the logarithmic function exists.
Similarly this works for the given function which is $\ln \left( {3x - 1} \right)$, consider this as given below:
$\Rightarrow y = \ln \left( {3x - 1} \right)$
Here also the given function of the logarithmic function, which is in terms of $x$, this logarithmic function exists, only when the function in $x$ is greater than zero.
$\Rightarrow \left( {3x - 1} \right) > 0$
Simplifying the value of $x$, as given below:
$\Rightarrow 3x > 1$
$\Rightarrow x > \dfrac{1}{3}$
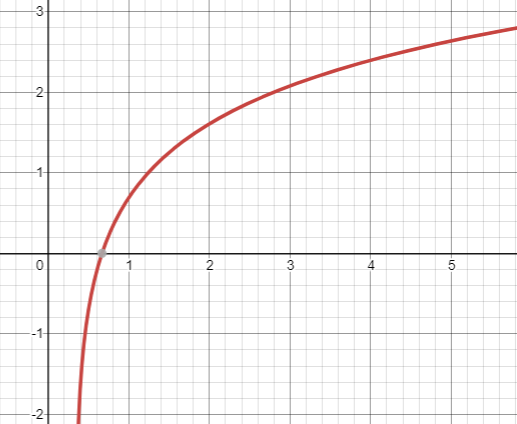
So the interval of which $\ln \left( {3x - 1} \right)$ is continuous is given by:
The vertical asymptote approaches $x = \dfrac{1}{3}$ and the function continues on towards positive infinity.

Note:
Please note that the function $f(x)$ is continuous when $x = c$ is the same as saying that the function’s two-side limit at $x = c$ exists and is equal to $f(c)$. A function $f(x)$ is right continuous at a point $c$ if it defined on an interval $\left[ {c,d} \right]$ lying to the right of $c$ and if $\mathop {\lim }\limits_{x \to {c^ + }} f(x) = f(c)$. Similarly it is left continuous at $c$ if it is defined on an interval $\left[ {d,c} \right]$ lying to the left of $c$ and if $\mathop {\lim }\limits_{x \to {c^ - }} f(x) = f(c)$.