Question

How do you find the intercepts of the line $y=5x-15$?

Answer 1

From the question given, we have been asked to find the intercepts of the line $y=5x-15$.We can find the intercepts by simply assuming the variables in the given line equation to be zero. To find the intercept of variable $x$ we have to assume that variable $y$ is equal to zero. And to find the intercept of variable $y$ we have to assume that variable $x$ is equal to zero.

Complete step by step answer:
Now considering from the question we need to find the intercepts of the given expression.
To find the $x$ intercept, we have to equal the variable $y$ to zero.
Therefore $y=5x-15$
Assume that $y=0$
$0=5x-15$
Now, shift $-15$ to the left hand side of the equation from the right hand side of the equation.
By shifting, we get $15=5x$
By rearranging it, we get $5x=15$
Shift $5$ to the right hand side of the equation from the left hand side of the equation.
By shifting, we get
$x=\dfrac{15}{5}$
$x=3$
Therefore $x$ intercept is $\left( 3,0 \right)$

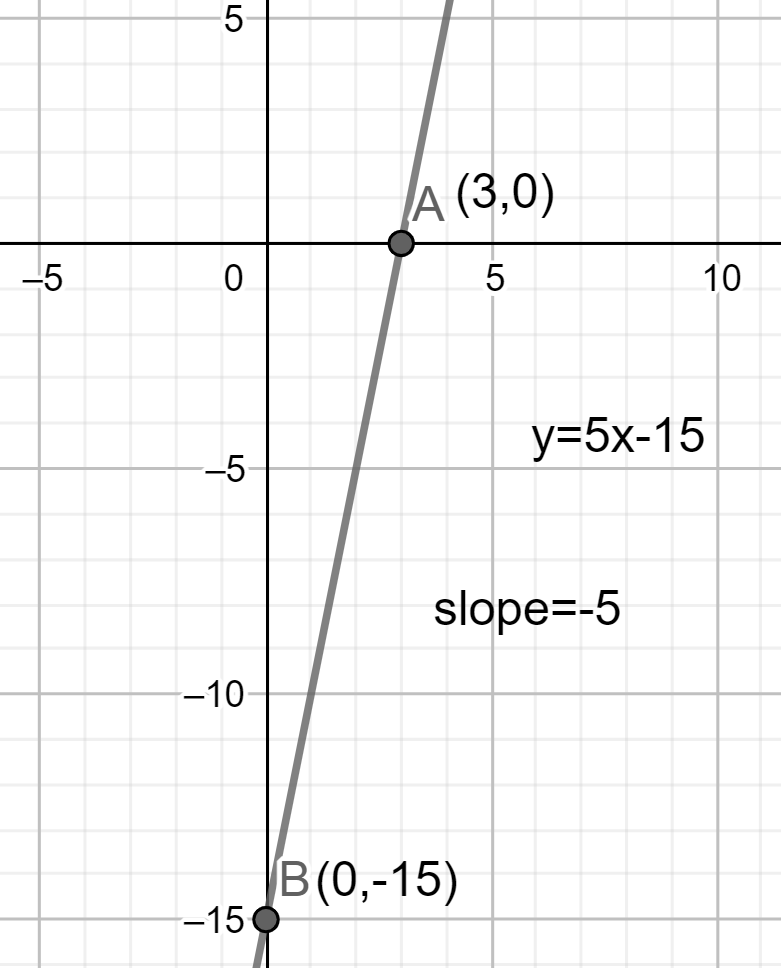
Now, we have to find the $y$ intercept.
As we have already discussed above, to find the $y$ intercept, we have to equate the variable $\x$ to zero.
By doing this we get, $y=5x-15$
Assume that $x=0$.
$y=5\left( 0 \right)-15$
$y=-15$
Therefore, $y$ intercept is $\left( 0,-15 \right)$.
Hence, we got the intercepts for the given line equation.

Note:
We should be well aware of the concepts of slope and intercepts. Also, we should be very careful while doing the calculation for this problem. Also, we should be careful while assuming and substituting it in the given line equation. Also, we should be well known about finding the intercepts of a given line equation. We can also find the slope of the given expression using the intercepts the formulae is given as $\dfrac{\text{y-intercept}}{\text{x-intercept}}$ for this equation it is $m=\dfrac{-15}{3}\Rightarrow -5$ .