Question

How do you find the important points to graph $f(x) = \dfrac{1}{{x - 3}}$?

Answer 1

In the given equation, we are given an equation and we are asked to find the important points of the given equation. To get the y-intercept we will put x=0 and then to get the x-intercept we will put y=0. Since, we have the main points of the given equation, we can plot the required graph.

Complete step by step answer:
Given that, the function $f(x) = \dfrac{1}{{x - 3}}$ we need to find the important points of the graph i.e. domain, range, standard form of the equation, non-defined points, etc.

First, we have to find the Domain of the function (${D_f}$):
And for this, the denominator of the function should not become zero.
When the denominator of the function approaches 0, the function approaches infinity.
$\Rightarrow x - 3 \ne 0$
$\Rightarrow x \ne 3$

Here, ${D_f}:x \in R - \\{ 3\\}$
Thus, $x \to 3 \Rightarrow f(x) \to \infty$

Second, we should check the Range of the function (${R_f}$):
Let, $y = \dfrac{1}{{x - 3}}$
$\Rightarrow yx - 3y = 1$
$\Rightarrow yx = 1 + 3y$
$\Rightarrow x = \dfrac{{1 + 3y}}{y}$
Here, ${R_f}:y \in R - \\{ 0\\}$
Thus, $y \to 0 \Rightarrow x \to \infty$

Next, we should check for the standard form of equation:
Let, $y = \dfrac{1}{{x - 3}}$
$\Rightarrow yx - 3y = 1$
$\Rightarrow yx = 1 + 3y$
$\Rightarrow xy = 1 + 3y$
It resembles $xy = c$ which is the equation for the rectangular hyperbola.
Thus, this equation is in the standard form of rectangular hyperbola.

Also, we will find important points by finding the intercepts (both x and y).
(a) When $x = 0$

$f(x) = \dfrac{1}{{x - 3}}$

$\Rightarrow f(0) = \dfrac{1}{{0 - 3}}$
$\Rightarrow f(0) = - \dfrac{1}{3}$
Here, the y – intercept is $0$.
Thus, the co-ordinates we get are $(0, - \dfrac{1}{3})$.
(b) Let $y = \dfrac{1}{{x - 3}}$
When $y = 0$
$\Rightarrow 0 = \dfrac{1}{{x - 3}}$
$\Rightarrow 0 = 1$ which is not possible.
This means, when $y=0$, $x$ value can’t be determined.
The graph of the function $f(x) = \dfrac{1}{{x - 3}}$ will look like this:

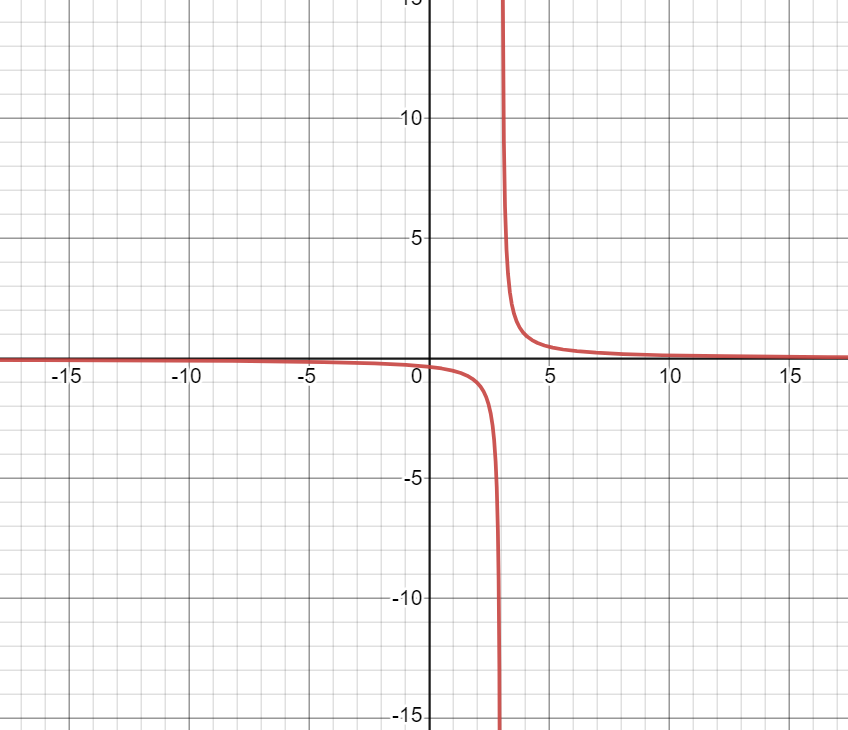
Note:

In the above graph, when $y=0$, the value of $x$ seems to be approaching zero but it is not zero.
The intercepts should be correctly known and accordingly only the graph will come out correctly. Also, the equation $y = {x^2}$ gives the parabola which is open upwards. And, for the equation $y = - {x^2}$ gives the parabola which is open downwards. We can find the vertex point by making the given equation in the form of the standard equation of the parabola.