Question

How do you find the focus, vertex and directrix of ${x^2} = 32y$?

Answer 1

The equation is second degree in one variable $y$ and first degree in another variable $x$. Such an equation is of a parabola. We can find the focus, vertex and directrix using the standard form of the equation of parabola ${(x - h)^2} = 4a(y - k)$. In this equation, the vertex is $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$, focus is at a distance $a$ units from $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$ along the axis of the parabola, i.e. the focus is $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k + a)$, and the directrix is a straight line perpendicular to the axis of the parabola situated at $a$ units from $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$on the opposite side of the focus, i.e. equation of the directrix is given by, $y = k - a$.

Complete step by step solution:
The given equation is ${x^2} = 32y$. Since we have the equation in the second degree of exactly one variable, the given equation is of a parabola. To find the focus, vertex and the directrix we transform it into the standard form of the equation of the parabola ${(x - h)^2} = 4a(y - k)$.
We can write,

$$\Rightarrow {x^2} = 32y \\\ \Rightarrow {(x - 0)^2} = 4 \times 8 \times (y - 0) \\\$$

Therefore, $h = 0$, $k = 0$ and $a = 8$.
The vertex of the given parabola is $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$, i.e. the vertex is $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$
The focus is $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k + a)$, i.e. the focus is $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0 + 8)$ or $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 8)$
The equation of the directrix is given by $y = k - a$, i.e. the directrix is $y = 0 - 8$ or $y = - 8$.
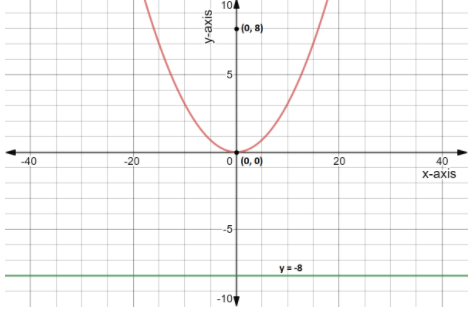
Hence, for the given equation we get the vertex is $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0)$, the focus is $(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 8)$ and the directrix is $y = - 8$.

This is also shown in the graph,

Note: The vertex and focus of the parabola both lies on the axis of the parabola. The line of the directrix is perpendicular to the axis of the parabola. For an equation in second degree in $y$ we use the standard form of the equation as ${(y - k)^2} = 4a(x - h)$ where the vertex is $(h,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$, the focus is $(h + a,{\kern 1pt} {\kern 1pt} {\kern 1pt} k)$ and the directrix is $x = h - a$.