Question

How do you find the focus and directrix of ${{x}^{2}}=2y$?

Answer 1

To find the focus and directrix of the parabola ${{x}^{2}}=2y$, first of all we will write this parabolic equation in the standard form of the parabola which is ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$. Now, in this parabolic equation, the focus of the parabola is $\left( h,k+a \right)$ and the directrix of a parabola is equal to: $y=k-a$.

Complete step-by-step answer:
The equation given in the above problem which we have to find the focus and directrix is as follows:
${{x}^{2}}=2y$
As you can see that the degree of the above equation is 2 so the above equation is a parabolic equation. And the parabola given above is symmetric with respect to y axis. And we know the coordinates of the focus of the parabola ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$:
$\left( h,k+a \right)$
Now, comparing the given parabola with the parabola ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$ which we have shown above we get:
${{x}^{2}}=2y$
${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$
As you can see that $\left( h,k \right)$ is equal to $\left( 0,0 \right)$ which we have proved as follows:
${{\left( x-0 \right)}^{2}}=2\left( y-0 \right)$
And to find the value of $''a''$ we are equating 2 to $4a$ we get,
$\Rightarrow 2=4a$
Dividing 4 on both the sides we get,
$\begin{aligned} & \Rightarrow \dfrac{2}{4}=\dfrac{4a}{4} \\\ & \Rightarrow \dfrac{1}{2}=a \\\ \end{aligned}$
Hence, we have found the value of $a=\dfrac{1}{2}$ and also $\left( h,k \right)=\left( 0,0 \right)$.
Now, the focus of the given parabola is equal to:
$\left( h,k+a \right)$
Substituting the values of $h,k,a$ which we have solved above in the above coordinates we get the value of focus as:
$\begin{aligned} & \Rightarrow \left( 0,0+\dfrac{1}{2} \right) \\\ & \Rightarrow \left( 0,\dfrac{1}{2} \right) \\\ \end{aligned}$
Hence, the focus of the parabola given in the above problem is equal to $\left( 0,\dfrac{1}{2} \right)$.
Now, we know the directrix for parabola ${{\left( x-h \right)}^{2}}=4a\left( y-k \right)$ is as follows:
$y=k-a$
Substituting the values of $k\And a$ which we have calculated above in the above equation we get,
$\begin{aligned} & \Rightarrow y=0-\dfrac{1}{2} \\\ & \Rightarrow y=-\dfrac{1}{2} \\\ \end{aligned}$
Hence, we have calculated the equation of directrix of the above parabola is as follows:
$y=-\dfrac{1}{2}$
We have shown the focus and directrix on the graph as follows:

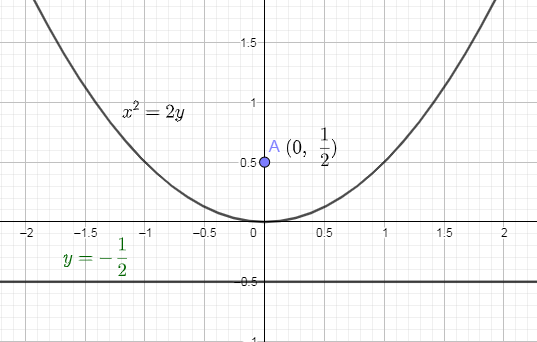
In the above graph, point A is showing the coordinates of the focus and we have also shown the equation of a directrix.

Note: The common mistake that could be possible in the above problem is that you might confuse the above parabola with the following parabola:
${{y}^{2}}=4ax$
The parabola which we have just written is symmetric about x axis so you might think that the parabola given in the above problem i.e. ${{x}^{2}}=2y$ is same as the parabola which we have written above and then the coordinates of the focus and the directrix will get wrong because you will write focus and directrix with respect to ${{y}^{2}}=4ax$.