Question

How do you find the exact values $\sin \left( {\dfrac{\pi }{4}} \right)$ using special triangles?

Answer 1

To solve this problem we have to know what a special triangle really means and then by knowing that we have to derive the general value for the hypotenuse and opposite side using the Pythagoras theorem. And at last substitute the value in $\sin = \dfrac{{opp}}{{hyp}}$.

Complete step by step answer:
To solve this problem, first we must understand the concept of a special triangle. Special triangle is nothing but a right angle triangle where the adjacent side and opposite side are equal. And they have three angles which is $45 - 45 - 90$, where two angles will be equal.

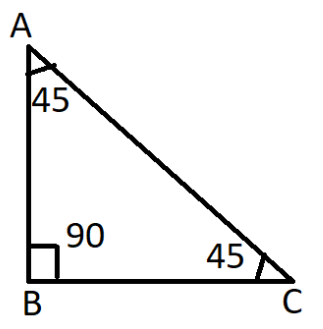
We have a $\angle ABC$ where $AB = BC$; in a $45 - 45 - 90$ triangle, always the adjacent is equal to the opposite side. Now let us consider $AB = BC = x$. By applying Pythagora's theorem, we can find the value of the hypotenuse side. The Pythagoras theorem states that the square of the hypotenuse side is equal to the sum of squares of the other two sides. By applying the theorem, we get,
$\Rightarrow A{C^2} = A{B^2} + B{C^2}$
$\Rightarrow A{C^2} = {x^2} + {x^2}$
$\Rightarrow A{C^2} = 2{x^2}$
$\Rightarrow AC =$ $\sqrt 2 x$
We got the value for hypotenuse side and we know that the formula for the $\sin \theta = \dfrac{{opp}}{{hyp}}$ and by the theorem we have already found the value for hypotenuse side, by substituting the values we get,
$\Rightarrow \sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{x}{{\sqrt 2 x}}$
$\Rightarrow \sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$
This is our required answer.

Note: In a special triangle, there are two models one is $45 - 45 - 90$ and the other one is $30 - 60 - 90$. In this problem we have chosen the $45 - 45 - 90$ triangle because the value given in the question is $\dfrac{\pi }{4}$ which is ${45^\circ }$. The $30-60-90$. triangle differs from the other. Both are not the same.