Solveeit Logo
Login

Question

Question: How do you find the exact values of \({{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)\)?...

How do you find the exact values of sin⁡−1(22){{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)?

Explanation

Solution

In this problem, we have to find the value of the angle given. We will be using trigonometric ratios and some properties of inverse functions. Trigonometric functions will be applied on the right angled triangle with given sides and angles. Mainly we have to solve the whole question using Pythagoras theorem:
(hypotenuse)2=(base)2+(perpendicular)2{{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}
Now, solve the problem and find its solution.

Complete step-by-step answer:
Here, the basic function of the trigonometry is used i.e. sine. Even some functions can be derived using this function. They are:
⇒\Rightarrow cosecθ\theta = 1sin⁡θ\dfrac{1}{\sin \theta }
⇒\Rightarrow secθ\theta = 1cos⁡θ\dfrac{1}{\cos \theta }
⇒\Rightarrow tanθ\theta = sin⁡θcos⁡θ\dfrac{\sin \theta }{\cos \theta } = 1cot⁡θ\dfrac{1}{\cot \theta }
⇒\Rightarrow cotθ\theta = 1tan⁡θ\dfrac{1}{\tan \theta } = cos⁡θsin⁡θ\dfrac{\cos \theta }{\sin \theta }
Let’s see how we actually find the angle of a triangle using sine function.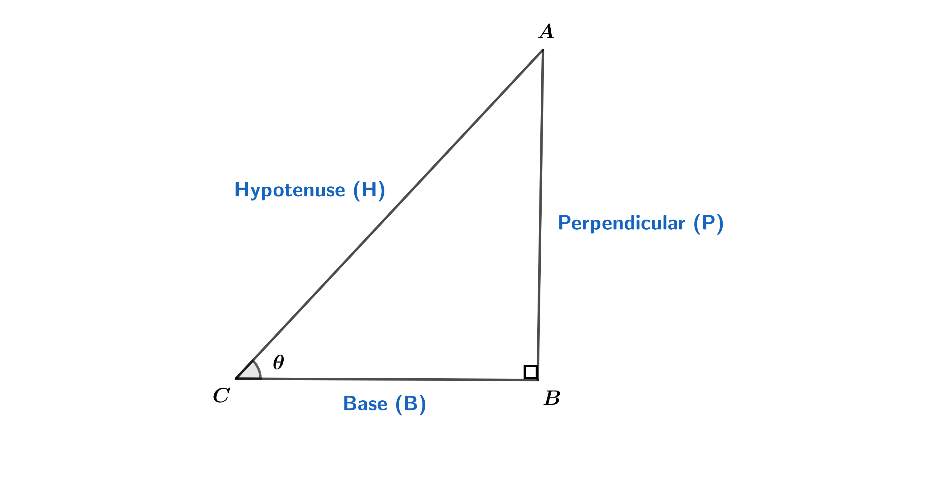
So, from figure, sinθ\theta = perpendicular(P)hypotenuse(H)\dfrac{perpendicular(P)}{hypotenuse(H)}
Let’s assume a triangle which is right angled at B. It’s sides are 22,22\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} and 1. Angles are: ∠A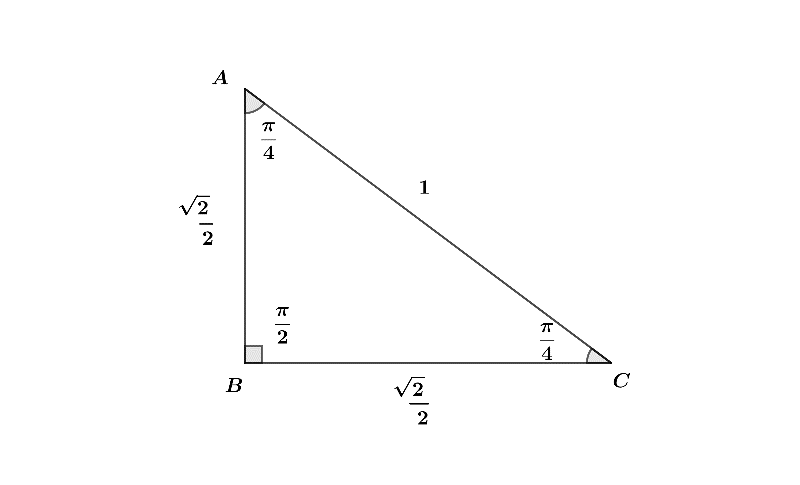=π4,∠B=π2,∠C=π4\angle A=\dfrac{\pi }{4},\angle B=\dfrac{\pi }{2},\angle C=\dfrac{\pi }{4}
Let’s check whether the triangle satisfies Pythagoras theorem or not. According to Pythagoras theorem:
(hypotenuse)2=(base)2+(perpendicular)2{{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}
⇒(AC)2=(BC)2+(AB)2\Rightarrow {{\left( AC \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}
Now, put the values for base and perpendicular:
⇒(AC)2=(22)2+(22)2\Rightarrow {{\left( AC \right)}^{2}}={{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{2}}{2} \right)}^{2}}
Open the brackets and solve:
⇒(AC)2=24+24\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{2}{4}+\dfrac{2}{4}
On adding, we get:
⇒(AC)2=44\Rightarrow {{\left( AC \right)}^{2}}=\dfrac{4}{4}
Cancel the like terms:
⇒AC=1\Rightarrow AC=\sqrt{1}
∴\therefore AC = 1
Which proves that it satisfies Pythagoras theorem.
As we know that, sinθ\theta = perpendicular(P)hypotenuse(H)\dfrac{perpendicular(P)}{hypotenuse(H)}
According to the triangle,
⇒sin⁡(π4)=22\Rightarrow \sin \left( \dfrac{\pi }{4} \right)=\dfrac{\sqrt{2}}{2}
When we take to the other side, it will form an inverse function. So,
⇒π4=sin⁡−1(22)\Rightarrow \dfrac{\pi }{4}={{\sin }^{-1}}\left( \dfrac{\sqrt{2}}{2} \right)
So we get the value as π4\dfrac{\pi }{4}.

Note: Here, Pythagora's theorem is just used to check whether we have taken right sides and angles for right angled triangle or not. As we know that trigonometric functions work only on right angled triangles. Knowledge of basic trigonometric functions is very much necessary for solving such questions.