Solveeit Logo
Login

Question

Question: How do you find the exact value of \(\tan x - 3\cot x = 0\) in the interval \(0 \leqslant x < 360? \...

How do you find the exact value of tan⁡x−3cot⁡x=0\tan x - 3\cot x = 0 in the interval 0⩽x<360?0 \leqslant x < 360?

Explanation

Solution

Here we take 3 cot⁡ x3\,\cot \,x on the right-hand side and use the identity cot⁡ x= 1tan⁡ x\cot \,x = \,\dfrac{1}{{\tan \,x}} . Then solve the equation to get the range of values of xx . We know that tan⁡ 60∘ = 3\tan \,{60^ \circ }\, = \,\sqrt 3 and rest can be found using the identities.

Formula used: The following formula is used:
cot⁡ x= 1tan⁡ x\cot \,x = \,\dfrac{1}{{\tan \,x}}

Complete step-by-step solution:
The main equation can be written as:
tan⁡ x − 3 cot⁡ x =0\tan \,x\, - \,3\,\cot \,x\, = 0
Transposing 3cot⁡x3\cot x on the right-hand side.
tan⁡ x = 3 cot⁡ x\tan \,x\, = \,3\,\cot \,x
Using the formula, we get:
tan⁡ x = 3×1tan⁡ x\tan \,x\, = \,3 \times \dfrac{1}{{\tan \,x}}
tan⁡ 2x = 3\tan {\,^2}x\, = \,3
Taking the square roots on both the sides.
Now, tan⁡ x = 3 ortan⁡ x = −3\tan \,x\, = \,\sqrt 3 \,or\tan \,x\, = \, - \sqrt 3
Hence, x =60∘ + k.180∘x\, = {60^ \circ }\, + \,k{.180^ \circ }
Or it can be written in the form of x = 120∘ + k. 180∘x\, = \,{120^ \circ }\, + \,k.\,{180^ \circ } where kk is an integer.
Now, we can take all the values of xx that lie between 0∘ and 360∘{0^ \circ }\,and\,{360^ \circ }

Therefore x\, \in \,\left\\{ {{{60}^ \circ },\,{{120}^ \circ },\,{{240}^ \circ },\,{{300}^ \circ }} \right\\}

Note: There are three main functions in trigonometry i.e. Sine, Cosine and Tangent. There are certain trigonometric identities which can be stated as below:
sin⁡x = 1cos⁡ec x\sin x\, = \,\dfrac{1}{{\cos ec\,x}}
cos⁡x = 1sec⁡ x\cos x\, = \,\dfrac{1}{{\sec \,x}}
tan⁡x =1cot⁡x\tan x\, = \dfrac{1}{{\cot x}}
Trigonometric equations are those equations which contain trigonometric functions i.e. Sine, Cosine, Tangent, Cosecant, Secant and Cotangent.
The graph for the above equation tan⁡ x − 3 cot⁡ x =0\tan \,x\, - \,3\,\cot \,x\, = 0 can be shown as below:

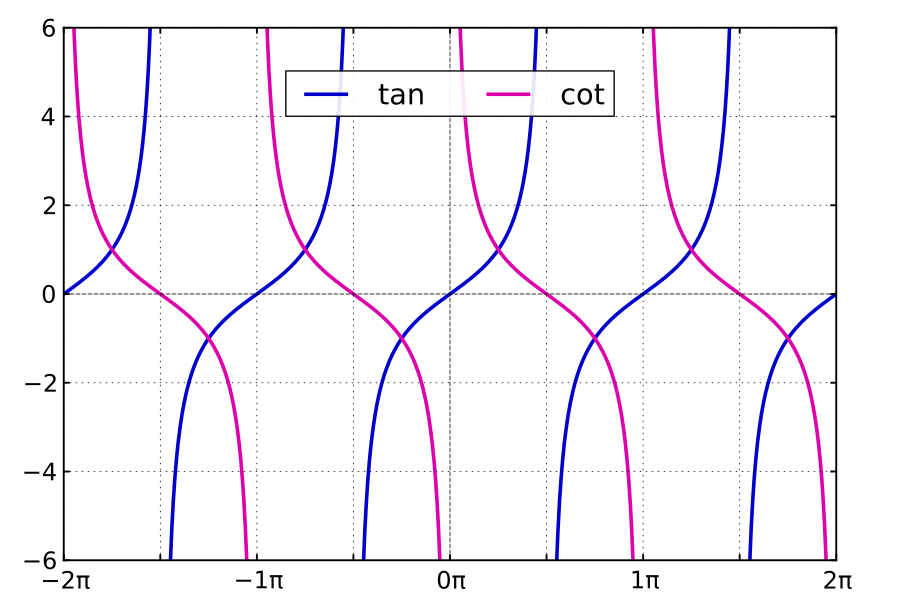
The graph shows that tan⁡ x\tan \,x and cot⁡ x\cot \,x meet at 44 different points in the range of 0∘ and 360∘{0^ \circ }\,and\,{360^ \circ } .
All the trigonometric identities are periodic functions of 2π2\pi .
That means for every integer kk, it can be written as follows:
sin⁡ (x + 2kπ) = sin⁡ x\sin \,(x\, + \,2k\pi )\, = \,\sin \,x
cos⁡ ( x + 2kπ) = cos⁡ x\cos \,(\,x\, + \,2k\pi )\, = \,\cos \,x
tan⁡ (x + kπ) = tan⁡ x\tan \,(x\, + \,k\pi )\, = \,\tan \,x