Solveeit Logo
Login

Question

Question: How do you find the exact value of \(\tan \left( {\dfrac{\pi }{3}} \right)\)?...

How do you find the exact value of tan⁡(π3)\tan \left( {\dfrac{\pi }{3}} \right)?

Explanation

Solution

Here we can proceed by finding the sin⁡ and cos\sin {\text{ and cos}} of the same angle as given and we know that tan⁡x=sin⁡xcos⁡x\tan x = \dfrac{{\sin x}}{{\cos x}} and therefore we can divide both the values of the sin⁡ and cos\sin {\text{ and cos}} of the same angle and get the exact value of the tan⁡(π3)\tan \left( {\dfrac{\pi }{3}} \right).

Complete step-by-step answer:
Now we are given to find the exact value of tan⁡(π3)\tan \left( {\dfrac{\pi }{3}} \right)
We know that:
sin⁡(π3)=32\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{2} −−−−(1) - - - - (1)
cos⁡(π3)=12−−−−(2)\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{2} - - - - (2)
Now we can find the relation between sin⁡,cos⁡,tan⁡\sin ,\cos ,\tan to get the value of the tan⁡(π3)\tan \left( {\dfrac{\pi }{3}} \right)
Let us consider the triangle ABCABC right angled at BB

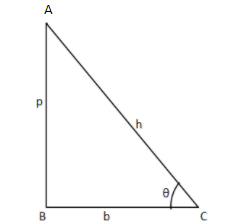
We know that:
sin⁡θ=perpendicularhypotenuse−−−−(3)\sin \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} - - - - (3)
cos⁡θ=basehypotenuse−−−−(4)\cos \theta = \dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}} - - - - (4)
We also know that:
tan⁡θ=perpendicularbase−−−−(5)\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} - - - - (5)
Now if we divide the equation (3) and (4) we will get:
sin⁡θcos⁡θ=perpendicularhypotenusebasehypotenuse=perpendicularbase\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}}}}{{\dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}}}} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}
Hence we get that:
sin⁡θcos⁡θ=perpendicularbase−−−−(6)\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} - - - - (6)
Now we can compare the equation (5) and (6) to get the required relation between sin⁡,cos⁡ and tan\sin ,\cos {\text{ and tan}}
On comparing both equation (5) and (6) we can say that:
tan⁡θ=\tan \theta = sin⁡θcos⁡θ\dfrac{{\sin \theta }}{{\cos \theta }}
So we know the value of sin⁡(π3)=32\sin \left( {\dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{2} and cos⁡(π3)=12\cos \left( {\dfrac{\pi }{3}} \right) = \dfrac{1}{2}
Now we know that:
tan⁡θ=\tan \theta = sin⁡θcos⁡θ\dfrac{{\sin \theta }}{{\cos \theta }}
Here putting the value of θ=π3\theta = \dfrac{\pi }{3} we get:
tan⁡π3=\tan \dfrac{\pi }{3} = sin⁡π3cos⁡π3\dfrac{{\sin \dfrac{\pi }{3}}}{{\cos \dfrac{\pi }{3}}} =3212=(3)(2)(1)(2)=3= \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}} = \dfrac{{(\sqrt 3 )(2)}}{{(1)(2)}} = \sqrt 3
Hence by this method we have got the exact value of the given trigonometric function which is tan⁡(π3)\tan \left( {\dfrac{\pi }{3}} \right)
So in order to calculate tangent of any angle we need to just divide the sin and cosine of the same angle and we will get the tangent of that angle as we know that:
tan⁡θ=\tan \theta = sin⁡θcos⁡θ\dfrac{{\sin \theta }}{{\cos \theta }}
So we get the value of tan⁡(π3)=3\tan \left( {\dfrac{\pi }{3}} \right) = \sqrt 3

Note: Here in these types of problems where we are asked to find the value of the tangent or cotangent of any angle, we must know the basic values of the sine and cosine of the angles like 0∘,30∘,45∘,60∘,90∘0^\circ ,30^\circ ,45^\circ ,60^\circ ,90^\circ and then we can easily calculate the same angles of the tangent, cotangent, secant and cosecant of that same angle.