Question

How do you find the exact value of $\sin \dfrac{\pi }{6}$ using the special triangles?

Answer 1

To find the exact value of given trigonometric function using special triangle, first find the other angle of the special triangle (special triangle have a right angle) and then draw a special triangle according to the interest of the question and label sides of that special triangle. Then use the definition of the given trigonometric ratio to find the answer.

Complete step by step solution:
In order to find the exact value of $\sin \dfrac{\pi }{6}$ using the special triangles, we will first find other two angles of the special triangle in order to draw to it,
Given angle: $\dfrac{\pi }{6}$ and also we know that a special triangle consists of a right angle.
Therefore according to properties of triangle, third angle will be given as
$x = \pi - \dfrac{\pi }{2} - \dfrac{\pi }{6} = \dfrac{\pi }{3}$
Now drawing the triangle,

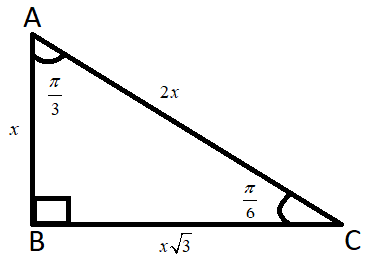
In the special triangle having angles $\dfrac{\pi }{6},\;\dfrac{\pi }{3}\;{\text{and}}\;\dfrac{\pi }{2}$, we know that its sides is given as in the figure.
Now from the definition of trigonometric ratios, we know that sine of an angle gives the ratio of height to hypotenuse, so we can write this for the above triangle as
$\sin \dfrac{\pi }{6} = \dfrac{{{\text{AB}}}}{{{\text{AC}}}} = \dfrac{x}{{2x}} = \dfrac{1}{2}$

Therefore we get the exact value of $\sin \dfrac{\pi }{6}$ equals to $\dfrac{1}{2}$

Note: There are some things to clear up. The way you phrased your question, it was a bit confusing. First of all, a triangle cannot be obtuse and acute at the same time. In this particular case, the triangle is acute. And the formulas like the identities and law of cosine and sine are important so make sure to remember them well.