Question

How do you find the exact value of sin (0)?

Answer 1

By definition, in a right−angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
sin θ = $\dfrac{P}{H}$ , cos θ = $\dfrac{B}{H}$ , tan θ = $\dfrac{P}{B}$ .
Recall that the Pythagoras' theorem holds true for every right−angled triangle: ${{P}^{2}}$ + ${{B}^{2}}$ = ${{H}^{2}}$ . If we assume one of the non-right-angles as θ and write an expression in terms of P, B and H for sin θ using the definition above, we will get the result. What happens to the values of P, B and H when θ = 0?

Complete step-by-step answer:
Let's say we have a right-angled triangle with the side opposite to the angle θ as P (perpendicular) and H as the hypotenuse. The third side, adjacent to the angle, calls it B (base).
It can be represented as follows:

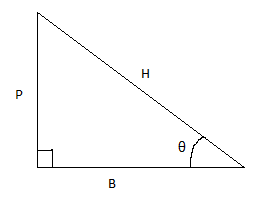
If the angle θ = 0 and if we maintain the right-angle (trigonometric ratios are defined for right angled triangles only), then the length of P will become 0 and H and B will coincide with each other, i.e. H = B.
We know that, because of the Pythagoras' theorem, ${{P}^{2}}$ + ${{B}^{2}}$ = ${{H}^{2}}$ . In this case also, ${{0}^{2}}$ + ${{B}^{2}}$ = ${{H}^{2}}$ , which is true, because B = H (since angle θ = 0).
By definition, sin θ = $\dfrac{Perpendicular}{Hypotenuse}$ = $\dfrac{P}{H}$ . Writing θ = 0 and substituting and P = 0, we get:
⇒ sin 0 = $\dfrac{0}{H}$
⇒ sin 0 = 0

Note: It can also be seen that cos 0 = $\dfrac{B}{H}$ = 1, because B = H.
There are many ways to prove the Pythagoras' theorem. For instance, it can be proved by using the properties of similar triangles, by drawing a perpendicular on the hypotenuse from the right-angled vertex and observing that the two smaller triangles have the same values of the angles and are thus similar.
It can also be observed from the right angled-triangle, that sin ( $90{}^\circ$ − θ) = cos θ etc.
Using the Pythagoras' theorem, we can also show that ${{\sin }^{2}}\theta$ + ${{\cos }^{2}}\theta$ = 1.