Question
Question: How do you find the exact value of \[\cos \dfrac{{33\pi }}{4}\]?...
How do you find the exact value of cos433π?
Solution
Given the expression in trigonometric form. First, write the measure of an angle as a sum of two angles. Now, we will use the Pythagorean Theorem to calculate the third side of the triangle with unit distance. Then, apply the cosine formula to substitute the value of the measure of angle into the expression.
Formula used:
The cosine formula for cos theta is given as:
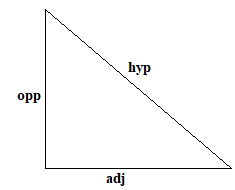
cosθ=hypadj
The Pythagorean Theorem states that the sum of squares of two smaller sides of the right triangle is equal to the square of the third side called hypotenuse.
Complete step-by-step answer:
We are given the measure of the angle. Now, we will write the angle 433π as a sum of two angles.
⇒cos433π=cos(432π+4π)
Again we will rewrite the term 432π as product of constant and 2π, we get:
⇒cos433π=cos(4×2π+4π)
Since 2π shows the complete circle which means 2π=0. Therefore, substitute the value of 2π.
⇒cos433π=cos(4×0+4π)
⇒cos433π=cos(4π)
Now, compute the value of hypotenuse in the triangle if the value of adjacent and opposite sides represents the unit circle using the Pythagorean Theorem.
hyp2=opp2+adj2
Now substitute the values into the formula.
hyp2=12+12
On simplifying the expression, we get:
⇒hyp2=2
We will take square root at both sides, we get:
⇒hyp=2
Now, we will apply the cosine formula to compute the value of cos(4π).
⇒cos(4π)=21
Hence the exact value of cos433π is 21
Note:
In such types of questions the students mainly don't get an approach on how to solve it. In such types of questions students mainly make mistakes while applying the formula for finding the value of the trigonometric angle. In such types of questions, students mainly get confused to represent the angle as a sum of two angles.
