Question

How do you find the exact value of $\cos 180{\text{ degrees}} - \sin 180{\text{ degrees}}$

Answer 1

Hint : In order to solve this question, we will first find out the values of $\cos 180^\circ$ and $\sin 180^\circ$ .For this, we consider the unit circle in which the Cartesian plane is divided into four quadrants. And we know that the value ${\text{180\;degree}}$ takes place in the second quadrant. As the cosine value in the second quadrant is always negative and the sine value in the second quadrant is always positive. So, from the value of ${\text{cos0}}^\circ$ and ${\text{sin0}}^\circ$ we will obtain the values of $\cos 180^\circ$ and $\sin 180^\circ$ respectively. And finally substitute it in the given expression and get the desired result.

Complete step-by-step answer :
We are asked to find the exact value of $\cos 180{\text{ degrees}} - \sin 180{\text{ degrees}}$
So, first of all we will find out the values of $\cos 180^\circ$ and $\sin 180^\circ$
Let us consider the unit circle in which the Cartesian plane is divided into four quadrants.

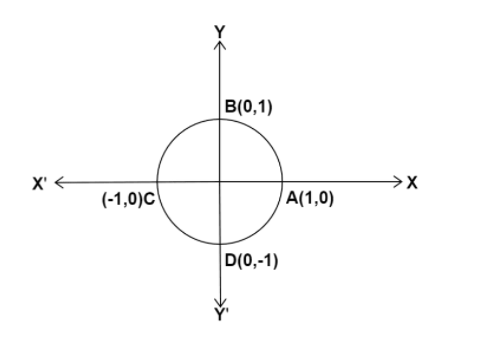
Now, we know that the value ${\text{180\;degree}}$ takes place in the second quadrant.
As the cosine value in the second quadrant always takes a negative value.
So, from the value of ${\text{cos0}}^\circ$ , we will obtain the value of $\cos 180^\circ$
We know that the exact value of ${\text{cos0}}^\circ$ is $1$
So, $\cos 180^\circ$ is $- \left( {\cos 0^\circ } \right)$ which is equal to $\left( { - 1} \right)$
Therefore, the value of $\cos 180^\circ = - 1$
Now the sine value in the second quadrant always takes a positive value.
So, from the value of ${\text{sin0}}^\circ$ , we will obtain the value of $\sin 180^\circ$
We know that the exact value of ${\text{sin0}}^\circ$ is $0$
So, $\sin 180^\circ$ is $+ \left( {\sin 0^\circ } \right)$ which is equal to $\left( { + 0} \right)$
Therefore, the value of $\sin 180^\circ = 0$
Now, we substitute the value of $\cos 180^\circ$ and $\sin 180^\circ$ in $\cos 180{\text{ degrees}} - \sin 180{\text{ degrees}}$
Therefore, we get
$\cos 180^\circ - \sin 180^\circ = - 1 - 0 = - 1$
Hence, the required exact value of $\cos 180^\circ - \sin 180^\circ$ is $-1$
So, the correct answer is “-1”.

Note : We can also explain this question in another way i.e.,
We know that within the unit circle, cosine provides the x coordinate of a point on the surface of the circle and sine provides the y coordinate of a point on the surface of the circle.
At $180^\circ$ the point on the unit circle surface is $\left( { - 1,0} \right)$ .So this means:
$x = \cos \left( {180^\circ } \right) = - 1$
$y = \sin \left( {180^\circ } \right) = 0$
So, the exact value of $\cos 180^\circ - \sin 180^\circ = - 1 - 0 = - 1$
Also, we can find the value of $\cos 180^\circ$ and $\sin 180^\circ$ in another way as,
$\sin \left( {180^\circ } \right) = \sin \left( {90^\circ + 90^\circ } \right)$
$\Rightarrow \sin \left( {180^\circ } \right) = \cos \left( {90^\circ } \right) = 0$
And $\cos \left( {180^\circ } \right) = \cos \left( {90^\circ + 90^\circ } \right)$
$\Rightarrow \cos \left( {180^\circ } \right) = - \sin \left( {90^\circ } \right) = - 1$