Question

How do you find the exact value of $arctan1\text{ or }{{\tan }^{-1}}1$?

Answer 1

tan$x$ is the ratio of $perpendicular$ to $base$ in a right angled triangle and if this ratio is $1$ that means the two sides are equal and using the property of an isosceles triangle their corresponding angles are also equal and that is $45{}^\circ$ each by applying the angle sum property.

Complete step by step solution:

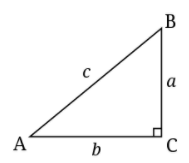
As we know that the $tangent$ function for acute angles can be viewed as the ratio of the opposite to the adjacent side of the angle.
$\Rightarrow \tan A=\dfrac{perpendicular}{base}=\dfrac{a}{b}$
Let the given value ${{\tan }^{-1}}1$ be $x$
$\Rightarrow {{\tan }^{-1}}1=x$
Now taking $\tan$both sides
$\Rightarrow \tan \left( {{\tan }^{-1}}1 \right)=x$
$\Rightarrow 1=\tan x$
If the ratio is 1, it means that the triangle is a right angle isosceles
Therefore, $m\angle A=m\angle B--(1)$
Now, using the angle sum property of the triangle
$\Rightarrow \angle A+\angle B+\angle C=\angle 180{}^\circ --(2)$
Since $\angle C=90{}^\circ --(3)$
From Equation $(1),(2),(3)$

& \Rightarrow \angle A+\angle B=90{}^\circ \\\ & \Rightarrow \angle A=\angle B=45{}^\circ \\\ \end{aligned}$$ And therefore the corresponding angle is $$45{}^\circ $$ degrees of $$\dfrac{\pi }{4}rad$$. **Hence, $$\arctan 1=\dfrac{\pi }{4}$$** **Note:** To find the exact value we will use the basic foundations of trigonometry. Normally for $$45{}^\circ $$ or $$\dfrac{\pi}{4} radian$$ and in general form $$(2n+1)\dfrac{\pi }{4}$$ where $$n\in Z$$ the length other two sides are equal and the domain of $$arctan1\text{ or }{{\tan }^{-1}}1$$ is $$\left[ -1,1 \right]$$ and the range is $$\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$$.