Solveeit Logo
Login

Question

Question: How do you find the equation of the tangent line to the graph of \(f\left( x \right)={{x}^{2}}+1\) a...

How do you find the equation of the tangent line to the graph of f(x)=x2+1f\left( x \right)={{x}^{2}}+1 at point (2,5)\left( 2,5 \right).

Explanation

Solution

In this problem we need to calculate the equation of the tangent to the curve f(x)=x2+1f\left( x \right)={{x}^{2}}+1 at point (2,5)\left( 2,5 \right). For this we need to calculate the slope of the tangent from the given curve. We know that the first order differentiation of the given curve with respect to xx will be the slope of the tangent at any point. To calculate the slope of the tangent at (2,5)\left( 2,5 \right) we will substitute the point (2,5)\left( 2,5 \right) in the slope of the tangent at any point. After getting the slope of the tangent at (2,5)\left( 2,5 \right), we will use the geometric formula that the equation of the line having slope mm and passes through the point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is (y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right). We will use this formula and simplify the equation to get the required solution.

Complete step by step answer:
Given curve f(x)=x2+1f\left( x \right)={{x}^{2}}+1
Differentiating the above equation with respect to xx, then we will get
⇒f′(x)=ddx(x2+1)\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{2}}+1 \right)
Applying derivation for each term individually, then we will have
⇒f′(x)=ddx(x2)+ddx(1)\Rightarrow {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( 1 \right)
We know that ddx(xn)=nxn−1\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}, ddx(a)=0\dfrac{d}{dx}\left( a \right)=0, then we will get
⇒f′(x)=2x+0 ⇒f′(x)=2x \begin{aligned} & \Rightarrow {{f}^{'}}\left( x \right)=2x+0 \\\ & \Rightarrow {{f}^{'}}\left( x \right)=2x \\\ \end{aligned}
Slope of the tangent at given point (2,5)\left( 2,5 \right) is given by
⇒m=2(2) ⇒m=4 \begin{aligned} & \Rightarrow m=2\left( 2 \right) \\\ & \Rightarrow m=4 \\\ \end{aligned}
Now the equation of the tangent or line having slope m=4m=4 and passes through the point (x1,y1)=(2,5)\left( {{x}_{1}},{{y}_{1}} \right)=\left( 2,5 \right) is
(y−5)=4(x−2)\left( y-5 \right)=4\left( x-2 \right)
Simplifying the above equation, then we will get
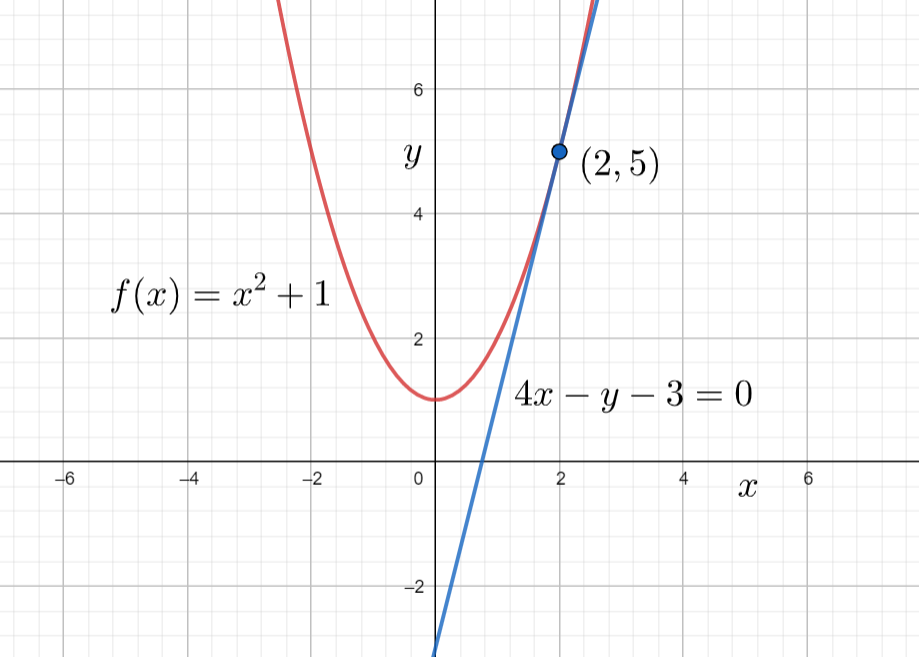
y−5=4x−8 ⇒4x−8−y+5=0 ⇒4x−y−3=0 \begin{aligned} & y-5=4x-8 \\\ & \Rightarrow 4x-8-y+5=0 \\\ & \Rightarrow 4x-y-3=0 \\\ \end{aligned}
Hence the tangent for the given curve is 4x−y−3=04x-y-3=0 and the graph of the tangent is shown in below

Note: In this problem they have only asked to calculate the equation of the tangent to the curve only. If they have asked to calculate the equation of the normal for the given curve, then we will take the slope of the normal as −1m-\dfrac{1}{m} and use the same geometric formula to calculate the equation of the normal.