Question

How do you find the equation of the parabola described with Vertex at $\left( {2, - 3} \right)$; focus at $\left( {2, - 5} \right)$?

Answer 1

We will use the normal equation of parabola in vertex form to find the equation of parabola with given focus and vertex. We know the equation of parabola having the axis along the $y$-axis is represented by the given equation ${x^2} = 4ay$, We know that the value of the $a = \pm \dfrac{1}{{4c}}$, where $c$ is the distance between vertex and focus of the parabola. If the $x$ coordinate in given focus $\left( {2, - 5} \right)$ and vertex $\left( {2, - 3} \right)$ is the same the parabola will be in the direction of vertical.

Formula used:
We can calculate the distance between the vertex and focus of the parabola. To find the distance between vertex and focus of the parabola, we will use the distance formula between two points, the distance between two points, formula is $\sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}}$. The equation of a parabola in vertex form is $x = a{\left( {y - k} \right)^2} + h$, where $h$ and $k$ is the vertex of the parabola. If the focus of the parabola lies downward to the parabola, then the parabola will open up towards the top.

Complete step by step solution:
The given vertex and focus of the parabola is $\left( {2, - 3} \right)$ and $\left( {2, - 5} \right)$.
Find the distance between vertex and focus of the parabola, by using the distance formula, which will be denoted by the symbol $a$ .
The two points of vertex and focus are $\left( {2, - 3} \right)$ and $\left( {2, - 5} \right)$.
$c = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}}$
Substitute the values in the formula.
$c = \sqrt {{{\left( { - 5 + 3} \right)}^2} + {{\left( {2 - 2} \right)}^2}}$
$\Rightarrow c = 2$
Find the value of $a$.
$a = \pm \dfrac{1}{{4 \times 2}}$
$\Rightarrow a = \pm \dfrac{1}{8}$
Since $a$ is negative in the question,
$\Rightarrow c = - \dfrac{1}{8}$
The vertex of the given parabola is $\left( {2, - 3} \right)$.
Therefore,
$h = 2$
$k = - 3$
Now substitute the value of vertex in the equation of parabola in vertex form.
The equation of parabola in vertex form is,
$x = a{\left( {y - k} \right)^2} + h$
$\Rightarrow x = - \dfrac{1}{8}{\left( {y + 3} \right)^2} + 2$
Final solution: Therefore, the given equation of parabola is $x = - \dfrac{1}{8}{\left( {y + 3} \right)^2} + 2$.

Note: You all are advised to use the distance formula carefully to avoid any mistake. You all must know the equation of a parabola in vertex form is given by the equation $x = a{\left( {y - k} \right)^2} + h$. You Must remember the value of $a = \pm \dfrac{1}{{4c}}$ where $c$ is the distance between vertex and focus of the parabola.
Diagram of parabola $x = - \dfrac{1}{8}{\left( {y + 3} \right)^2} + 2$:

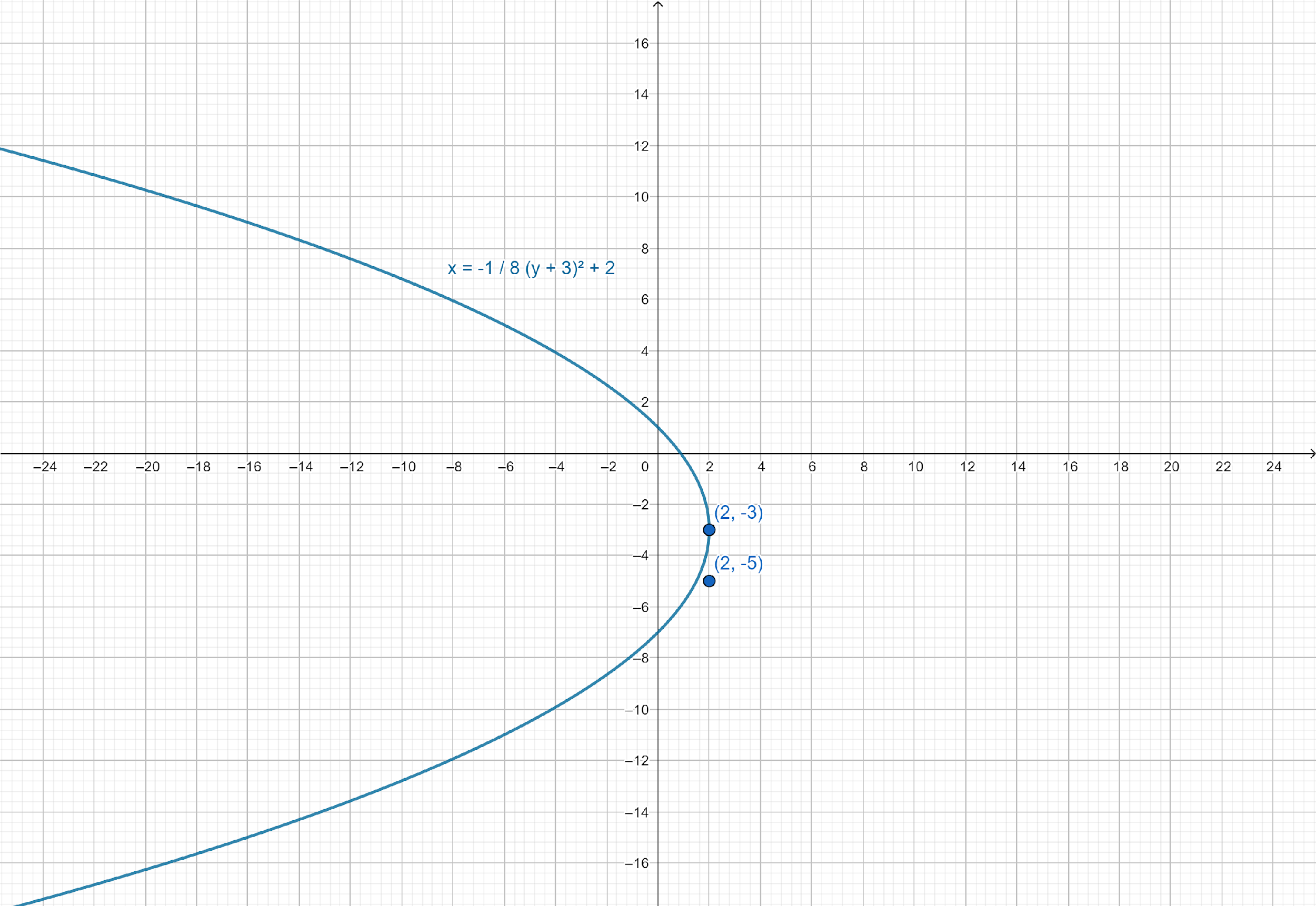
Parabola that opens left or right depending on the sign of a.
Our function is a parabola that opens to the left (a is negative).