Question

How do you find the equation of the line tangent to the graph of $y=\sin (x)$ at the point $x=\pi$ ?

Answer 1

For solving this type of problems, firstly we have to find the derivative of given function and after that substitute the value of given point to calculate the slope and then substitute the values of slope and intercept in the equation of a straight line and we will get our required equation of line tangent to graph.

Complete step-by-step solution:
Tangent can be defined as a line that touches any curve at any one point and does not cross through it and has the same instantaneous slope. The point where the curve and tangent meet is known as the point of tangency or the point of contact. The equation of the tangent line to any curve is the same as the equation of the straight line because the graph of tangent line represents the straight line.
Tangent approximates the curve at a point. They give the best approximation at that point by sowing the slope of the curve at that point.
As, we are given in the question $y=\sin (x)$
Now, we will differentiate this function with respect to $x$ because the derivative of any function represents the slope or gradient of the tangent line of that function at any point $x$
$\Rightarrow \dfrac{d}{dx}(y)=\dfrac{d}{dx}(\sin x)$
$\Rightarrow y'=\cos (x)$
Now for particular point ( i.e. $x=\pi$ ), we will substitute the value of $x$ in the derivative of function to get the slope
$\Rightarrow y'(\pi )=\cos (\pi )$
$\Rightarrow y'(\pi )=-1$
Now, we will find the point where our tangent touches the curve. If we substitute $x=\pi$ in our original function, then we will get the corresponding value of $y$
$y=\sin (x)$
$\Rightarrow y=\sin (\pi )$
$\Rightarrow y=0$
Since, a tangent is a straight line graph, so its equation can be defined as: $y=mx+c$ , where $m$ represents the slope of the line and $c$ is the $y$ intercept.
As, it has the slope $m=-1$ and passes through $({{x}_{0}}=\pi ,{{y}_{0}}=0)$ . So it becomes as:
$y=mx+c$
$\Rightarrow 0=(-1)(\pi )+c$
$\Rightarrow 0=-\pi +c$
$\Rightarrow c=\pi$
Now, substitute the value of $c$ and $m$ in equation of tangent line:
$\Rightarrow y=mx+c$
$\Rightarrow y=(-1)x+\pi$
$\Rightarrow y=-x+\pi$
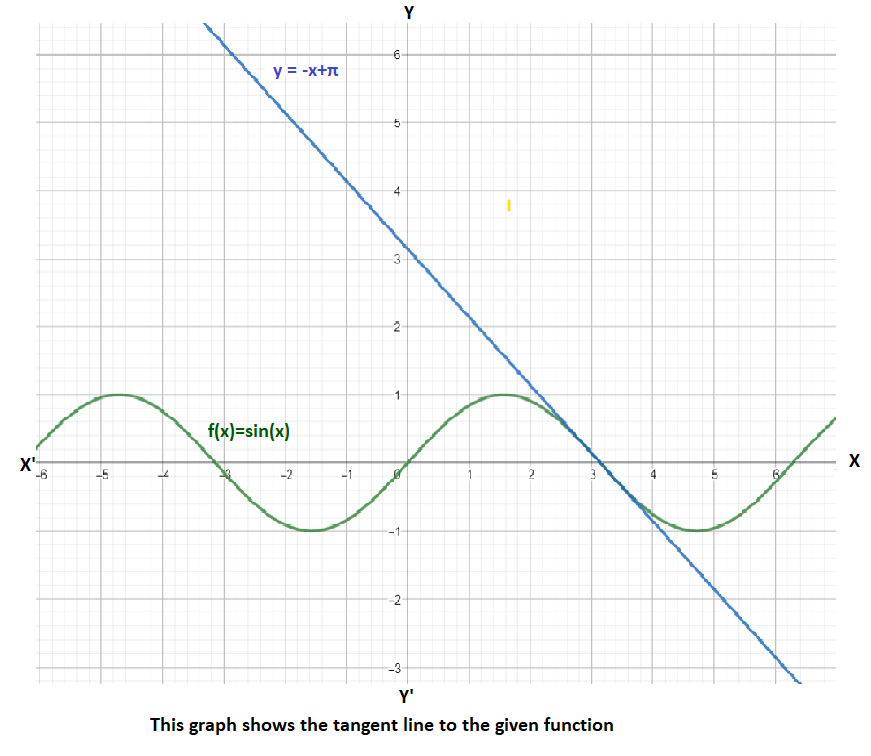
Therefore, the equation of the line tangent to the graph of $y=\sin (x)$ is: $y=-x+\pi$
Let’s see the graph of the equation of tangent line to the given function:

Note: A tangent to a circle is always perpendicular to the radius of that circle. The tangent line never crosses the circle, it just touches the circle. The angle which is formed by the tangent and a chord of a circle is the same as that of tangent inscribed on the opposite side of the chord.