Solveeit Logo
Login

Question

Question: How do you find the equation of the line tangent to the graph of \(f\left( x \right)={{x}^{2}}+5x\)....

How do you find the equation of the line tangent to the graph of f(x)=x2+5xf\left( x \right)={{x}^{2}}+5x. at x=4x=4?

Explanation

Solution

In this question we have to find the equation of a line which is tangent to the given graph. We will first substitute the value of x=4x=4 in the given function to get the point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right). we will then find the slope mm of the tangent by using the limit function. we will then use the slope-intercept form y−y1=m(x−x1)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right) and rearrange to get the required equation of the tangent.

Complete step-by-step answer:
We have the function given to us f(x)=x2+5xf\left( x \right)={{x}^{2}}+5x.
On substituting x=4x=4 in in the function, we get:
⇒f(4)=(4)2+5(4)\Rightarrow f\left( 4 \right)={{\left( 4 \right)}^{2}}+5\left( 4 \right)
On simplifying, we get:
⇒f(4)=16+20\Rightarrow f\left( 4 \right)=16+20
On adding the terms, we get:
⇒f(4)=36\Rightarrow f\left( 4 \right)=36
Therefore, the point is (x1,y1)=(4,36)\left( {{x}_{1}},{{y}_{1}} \right)=\left( 4,36 \right).
Now we know that the slope of the tangent line to a graph of a given function ff at x=ax=a is given by the limit lim⁡h→0f(a+h)−f(a)h\displaystyle \lim_{h \to 0}\dfrac{f\left( a+h \right)-f\left( a \right)}{h}
So, in this question, we have f(x)=x2+5xf\left( x \right)={{x}^{2}}+5x and a=4a=4, so the slope of the tangent line can be calculated as:
⇒lim⁡h→0f(4+h)−f(4)h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{f\left( 4+h \right)-f\left( 4 \right)}{h}
On substituting the function, we get:
⇒lim⁡h→0((4+h)2+5(4+h))−((4)2+5(4))h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{\left( {{\left( 4+h \right)}^{2}}+5\left( 4+h \right) \right)-\left( {{\left( 4 \right)}^{2}}+5\left( 4 \right) \right)}{h}
On simplifying the terms, we get:
⇒lim⁡h→016+8h+h2+20+5h−(16+20)h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{16+8h+{{h}^{2}}+20+5h-\left( 16+20 \right)}{h}
On simplifying the bracket, we get:
⇒lim⁡h→016+8h+h2+20+5h−16−20h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{16+8h+{{h}^{2}}+20+5h-16-20}{h}
On simplifying, we get:
⇒lim⁡h→08h+h2+5hh\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{8h+{{h}^{2}}+5h}{h}
On adding the similar terms, we get:
⇒lim⁡h→013h+h2h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{13h+{{h}^{2}}}{h}
Now on taking hh common in the numerator, we get:
⇒lim⁡h→0h(13+h)h\Rightarrow \displaystyle \lim_{h \to 0}\dfrac{h\left( 13+h \right)}{h}
Now since h→0h \to 0 and h≠0h\ne 0, on cancelling, we get:
⇒lim⁡h→0(13+h)\Rightarrow \displaystyle \lim_{h \to 0}\left( 13+h \right)
On putting the value of hh, we get:
⇒13\Rightarrow 13, which is the slope of the tangent line therefore m=13m=13.
Now to find the equation of the tangent, we will use the slope intercept form as:
⇒y−y1=m(x−x1)\Rightarrow y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)
On substituting (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) as (4,36)\left( 4,36 \right) and m=13m=13, we get:
⇒y−36=13(x−4)\Rightarrow y-36=13\left( x-4 \right)
On simplifying and rearranging the terms, we get:
⇒y=13x−16\Rightarrow y=13x-16, which is the required equation for the tangent.
On drawing the function and the tangent on the graph, we get:

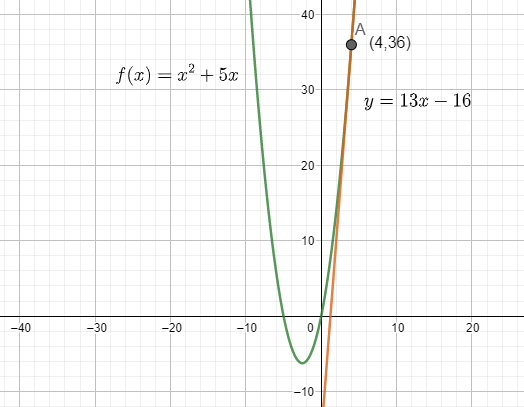
Which is the required solution.

Note: It is to be remembered that a tangent is a line segment which touches the given other curve on the graph through a point. The slope of the line mm tells us the steepness of the line. Slope of the line is also called the gradient of the line. It is to be remembered in limits that hh should not be substituted in the denominator such that 00 is present in the denominator.